next up previous contents index
Next: 7.5 SWS Pipeline Software Up: 7. Standard Product Generation Previous: 7.3 From SPD to

Subsections


7.4 Error Propagation in the SWS Pipeline

The ideas expounded in this section stem from a dissatisfaction with the way the error values were originally delivered to the users: one error tag which comprised the full gamut of systematic and random errors. The systematic errors almost always swamped the random ones. More importantly, it prevented the use of the statistical errors as weights in further processing. It was decided to keep three separate error tags in the AAR, one for the statistical errors and two for the more systematic offset and gain errors. This allows the use of the statistical error in various weighting and clipping schemes, which proved fruitful especially at low flux levels (Valentijn & Thi 2000, [38]).

These three tags are not the only source of quality in the SWS products. There is also the flag (SWAAFLAG and SWSPFLAG, see Table A.7) which provides information about the number of glitches detected within the reset interval. It also holds information whether the flux within the reset interval was (partially) out of limit. And there is the SWAATINT tag, see Section A.4.1.2, which contains the number of valid samples within the reset interval. Both glitches and out-of-limit samples diminish the number of valid samples.

Error handling in Calibration Procedures (CAPs), used to derive calibration files and their error, are not discussed in this section.

Of course, some sources of error (e.g. residual fringes) are still present in several bands. The removal of those depends on careful post-pipeline processing.

7.4.1 Basic formalism

The basic formula which describes how the signal $ S$ is converted into flux $ F$ reads (see also Section 5.5):

$\displaystyle F = ( S - S_d ) \cdot G_{r} \cdot G_{f} \cdot G_{p} \cdot G_{c}$ (7.12)

where $ S_d$ is the signal of the dark current measurement(s), $ G_r$ is the `gain' due to the responsivity function, $ G_f$ is the flat-field factor, $ G_p$ is the photometric gain and $ G_c$ is the flux conversion.

To derive the error from this, Equation 7.12 can be rewritten a little, defining $ G = G_{r} \cdot G_{f} \cdot G_{p} \cdot G_{c}$, as:

$\displaystyle F = ( S - S_d ) \cdot G$ (7.13)

from which the total error in $ F$ can be found. Relative errors in a product add quadratically:

$\displaystyle \left( \frac{\sigma _{F}}{F}\right) ^{2}=\left( \frac{\sigma _{S-S_d}}{S-S_d}\right) ^{2}+\left( \frac{\sigma _{G}}{G}\right) ^{2}$ (7.14)

Multiplying Equation 7.14 by $ F^{2}$, and expanding $ \sigma_{S-S_d}$ properly, results in:

$\displaystyle \sigma _{F} = \sqrt{ ( G \cdot \sigma_{S} )^{2} + ( G \cdot \sigma_{d} )^{2} + ( ( S - S_d ) \cdot \sigma_{G} )^{2} }$ (7.15)

where $ \sigma_d$ is the error in the dark current signal.

The right hand side of Equation 7.15 consists of 3 terms below the square-root symbol. The first one is related to the standard deviation ( stdev) in the slopes. Each slope has its own individual stdev which is statistically independent from the others. These standard deviations can be used to assess the quality of the individual slopes. They have to be multiplied by the gain to play its (properly scaled) role in the total error definition of F. The second one is an offset error. It is related to the error in the dark current measurements and as such it is applied to all slopes between two embracing darks. This makes the error a highly correlated one. When the dark current measurement is wrong, all related fluxes are off by the same amount. It also has to be multiplied by the gain to get its contribution to the total error. The third one is a gain error. As is proper for a gain error, this one is stored as a relative error. It consists of four parts: errors in the responsivity function; in the flat-field factor; the photometric gain; and the flux conversion. All four are highly correlated errors and except for the photometric gain the others are even correlated over all SWS measurements, i.e. the errors are taken from calibration files which are applied to all observations. So errors in the responsivity function, the flat-field and in the flux conversion affect all observations in a similar way. To get the contribution of the (relative) gain error to the total flux error it has to be multiplied by the flux: $ F \cdot \sigma_{G}/G = ( S - S_d ) \cdot \sigma_{G}$.

In summary there are three errors, one statistical error and two systematic errors, which will be referred to as `offset' and `gain' errors.

7.4.2 Slope error

The error in the signal is calculated when deriving the slope over the rectified ramps, see Section 7.2.9. The standard method is used to calculate the error in the slope:

$\displaystyle \sigma _{S}=\sqrt{\frac{\chi ^{2}}{(N-2)} C_{ss}}$ (7.16)

The first factor on the right hand side is the standard deviation of a linear model fit, and the second factor is the amount that has to be assigned to the slope part of the model.

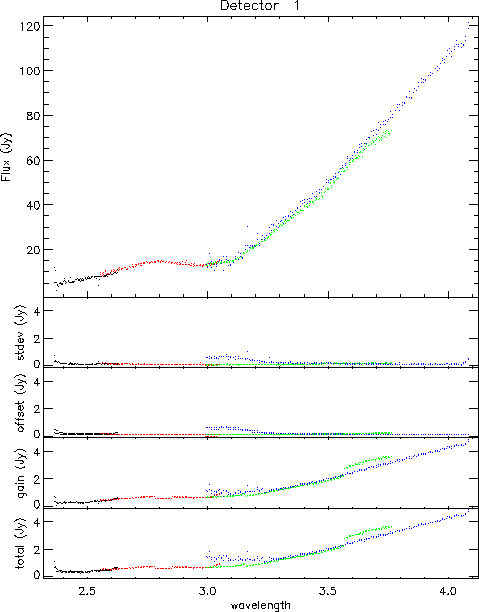
In Figure 7.12 an SPD is displayed with its slope errors, the dark current error, the number of glitches and the number of valid samples.

Figure 7.12: In the top panel we show the signal observed in detector 1 of an SPD. In the second panel is the standard deviation as was derived for this signal. In the third panel the (offset) error due to dark current subtraction is shown. The fourth panel shows the number of glitches found, not all that many in band 1. And in the lower panel the number of valid samples is shown. The actual dark current measurements are displayed in red.
\resizebox {12cm}{!}{\includegraphics{spd-errors.ps}}

7.4.3 Offset error

The error in the offset, $ \sigma_d$ is the error in the dark current, multiplied by the gain $ G$.

7.4.3.1 Standard dark current model

To calculate the dark current a preceding dark signal $ S_{1}$ at time $ t_{1}$, and one following, $ S_{2}$ at time $ t_{2}$ are necessary, see Sections 7.3.3 and referenced sections.

$\displaystyle S_d(t) = S_{1}\frac{t_{2}-t}{t_{2}-t_{1}} + S_{2}\frac{t-t_{1}}{t_{2}-t_{1}}$ (7.17)

It is a linear interpolation between $ S_{1}$ and $ S_{2}$. The error $ \sigma_d$ now becomes

$\displaystyle \sigma_d^{2} = \sigma_1^2 \left( \frac{t_2 - t}{t_2 - t_1} \right)^2 + \sigma_2^2 \left( \frac{t - t_1}{t_2 - t_1} \right)^2$ (7.18)

where $ \sigma_1$ and $ \sigma_2$ are the errors in both dark measurements. These errors were calculated as Median Absolute Deviates (MAD) to have a more robust estimate of the dark current error. A MAD can be converted into a standard deviation by division by 0.675, assuming the distribution is Gaussian within the FWHM.

When only one (preceding or following) dark measurement can be found, this dark is subtracted from the signal, and consequently the offset error equals the dark error.

Figure 7.12 shows the signal of detector 1 for an SWS01 SPD, together with the standard deviation of the signal, the offset error due to dark current subtraction, the number of glitches found and the number of valid samples.

7.4.3.2 Transients model in band 2

Band 2 is the only SWS band where a transients model was used to calculate the dark currents. Consequently the errors are also obtained in a different manner. The transients model has a number of parameters that have to be estimated, either for each individual observation or for the database as a whole. The latter are parameters that are assumed to be constant during the mission. See Section 7.3.3.2.

Each of the parameters has its own uncertainty and its own standard deviation. The errors in the dark current model were obtained from a MonteCarlo simulation of 25 cases where the optimal parameters are replaced by a random draw from a Gaussian distribution spanned by the covariance matrix of the model fit - see Kester 2001, [22].

An example of an offset error in band 2 is shown in Figure 9.4, lower panel, red line.

7.4.3.3 Comments

Both in the standard dark current subtraction and in the transient model it is assumed that the dark, or the zero level function in the transients model, changes linearly in time. Actually the standard dark can be seen as a no-model transient, using only the zero level function. This assumption of linearity entails the somewhat funny behaviour of Equation 7.18: it has a dip in the middle (Figure 7.12, middle panel), suggesting that the dark in between two dark measurements is somehow more certain than at the actual measurements. We do not think this is true. The true dark current makes its way from the first measurement to the second by some kind of random walk. We just assume that it is linear because of lack of information otherwise. We decided to keep Equation 7.18 to be mathematically correct.

7.4.4 Gain error

The gain error has four components, one from the responsivity function, one from the flat-field factor, one from the photometric gain and one from the flux conversion. To get the total gain error, the relative errors for the four components are added quadratically.

7.4.4.1 Responsivity error

The responsivity error is taken from calibration file Cal-G 25_xx, which has a separate entry where we estimate how good the RSRF is at that wavelength (see Figures 5.5 to 5.19). The RSRF is valid only for one resolution in wavelength. To accommodate the different resolutions possible with SWS, e.g. SWS01s at different speeds, we have to interpolate the RSRF to the proper resolution with a flux conserving interpolation scheme. See Section 5.4. It is assumed that the error follows the same integration formulae as the fluxes, except that the error is divided by the square root of a dilution factor being the ratio between FWHM and the local stepsize in wavelength. Integrating over more wavelengths yields a smaller error, while interpolating over a smaller part of a wavelength interval yields a larger error.

For the FP detectors the error fields in Cal-G 25_xx are not properly filled.

7.4.4.2 Flat-field error

The flat-field error is taken from the calibration file Cal-G 43. It is applied as is.

7.4.4.3 Photometric error

The photometric gain is obtained from fitting a model of a few fringes which are done during the photometric check to the data. This is done with a (robustified) least square fit. See Section 7.3.5.2. The photometric error follows from this fit as

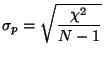$\displaystyle \sigma_p = \sqrt{ \frac{ \chi^2} {N-1} }$ (7.19)

The robustness of the procedure lies in one extra iteration where possibly outlying points are discarded.

7.4.4.4 Flux conversion error

The flux conversion is taken from the calibration file Cal-G 42. In that file also the flux conversion errors can be found.

An example of an AAR with all its pertaining errors is shown in Figure 7.13.

Figure 7.13: In the top panel we show the signal observed in detector 1 of an AAR as a function of wavelength. It is the same observation as in Figure 7.12. In the second panel we show the standard deviation as was derived for this signal, now converted into Jy. In the third panel the (offset) error due to dark current subtraction is shown, also converted to Jy. The fourth panel shows the gain error. In the lower panel all these errors are added together to form the total (systematic plus random) error in the observation. The four bands which comprises band 1, are colour-coded differently.
\resizebox {12cm}{!}{\includegraphics{aar-errors.ps}}

next up previous contents index
Next: 7.5 SWS Pipeline Software Up: 7. Standard Product Generation Previous: 7.3 From SPD to
ISO Handbook Volume V (SWS), Version 2.0.1, SAI/2000-008/Dc