This section presents a description of how the RSRF was measured during the Instrument Level Tests (ILT) (Feuchtgruber 2001, [9]) before launch, and how it was corrected based on in-orbit measurements of stellar calibration sources. The accuracy of the RSRF calibration is indicated and the remaining artifacts are discussed. More information on the calibration of the RSRF can be read in Vandenbussche et al. 2001, [41], and Vandenbussche 1999, [40].

5.4.1 RSRF measurements before launch

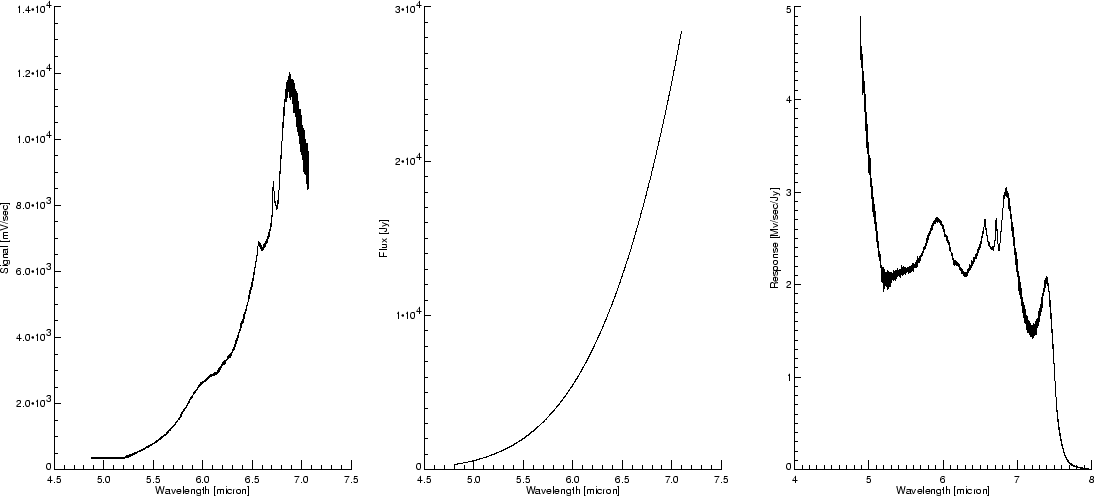
Prior to launch, the RSRF was determined during the instrument level tests. The measurements consisted of SWS spectra of a cryogenic blackbody calibration source at full spectral resolution, fully sampled in every detector. The calibration source fully filled the SWS apertures. Several scans were performed through the different SWS apertures and with blackbody temperatures ranging between 30 and 300 K. The spectra obtained were then divided by a Planck function of the corresponding blackbody temperature to obtain the RSRF. Figure 5.1 illustrates this calibration process.

**Figure 5.1:** Determining the RSRF from pre-launch SWS measurements of a blackbody in the lab. The left panel shows the response of an SWS detector during a scan in band 2B of a 173K blackbody. The middle panel shows a Planck curve for this blackbody temperature. The right panel shows the division of the two. This is the Relative Spectral Response for this detector in band 2B.
$\resizebox {\hsize}{!}{ \includegraphics{ilt_bbscan.ps} \includegraphics{planck173K.ps} \includegraphics{iltrsrf2b.ps}}$

5.4.2 In-orbit verification of the ILT RSRF

After launch, the accuracy of the ILT RSRF was verified by comparing SWS observations to synthetic spectra, composite spectra or template spectra for various sky calibration sources. This comparison revealed both broadband errors and small-scale errors.

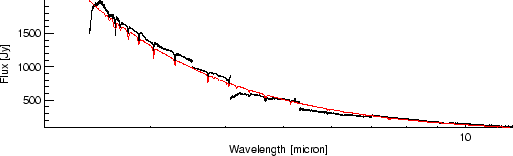
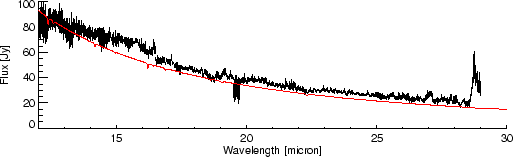
Figure 5.2 shows the broadband differences between a composite spectrum by Cohen et al. 1992a, [2], and an SWS observation of Sirius.

**Figure 5.2:** Comparison of a composite by Cohen et al. 1992a, [2], and the SWS spectrum of Sirius. The spectrum was calibrated with the RSRF derived from the pre-launch blackbody scans. Top: SW section; bottom: LW section.
$\resizebox {12cm}{!}{\includegraphics{sirius_iltrsrf_sw.ps}}$ $\resizebox {12cm}{!}{\includegraphics{sirius_iltrsrf_lw.ps}}$

Several effects e.g., differences in nature of calibration sources (extended vs point source), leaks in laboratory setup filters, diffraction losses and uncertainties or small drifts in the blackbody temperature, are responsible for the broadband errors in the pre-launch RSRF.

The SWS RSRF has been corrected for broadband differences between in-orbit observations and reference spectra, except for band 4, see Section 5.4.5.4. The quality of this correction improved in the course of the project as more SWS spectra of calibration stars were observed and the reference spectra available became more accurate.

5.4.3 Spline smoothing of residues

Fitting polynomes to the residues was clearly not optimal for the variety of shapes present in the residues. The problem with polynomial fits is that a local bias always translates to a global bias, e.g. strong oscillations in the high-order components of a polynomial fit to noisy data. Therefore a method of smoothing the residues with a cubic spline was adopted.

A spline function $S^{(m)}$ of order

with knots

is a set of functions

that are defined over the intervals [

], ... [ $x_{k-1}$ ,

] and stitched together in the knots so that the combined function

times continuously differentiable at the knots. The functions

are often cubic polynomes (n=3).

Späth et al. 1995, [36], describes various algorithms to smooth a dataset using splines. An algorithm has been adopted to smooth a dataset (

by determining a cubic spline $S^{(2)}$ for which $w_i(S^{(2)}(x_i)-y_i)^2 < P_i$ ,

are weights for the datapoints and

is a parameter for the smoothness in knot

and

are combined into one knot parameter

. Varying this parameter in a knot will result in a smoothing spline which is more 'stiff' or which follows the dataset more accurately in that region.

Cubic spline smoothing allows to make the correction curve follow the features in the residues where they are understood to be instrumental. In regions where the residues are believed to be unreliable (less accurately modelled features in the synthetic spectra, etc...) the spline smoothing curve is forced to be more 'stiff'. Therefore it is necessary that one understands the strong and weak points in the reference spectra and datasets used.

This method was implemented for every band and every detector as follows: for a selected set of calibration sources and reference spectra we calculated ratios (observation/model). The ratios are averaged over bins of $\lambda/\delta\lambda$ =200).

The data points in the average ratio are then taken as the knots for a cubic spline smoothing. The local stiffness of the smoothing spline is tuned in an Interactive Analysis widget tool, and the resulting spline is then evaluated in the wavelengths sampled in the ILT RSRF. These factors are multiplied with the responses in the ILT RSRF to obtain the corrected RSRF.

After carefully studying many sources observed by the SWS, four features in the residues (9-9.3, 10.1, 11.0 $\mu$ m in band 2C and at 12.3 $\mu$ m in band 3A) were understood as inaccuracies in the RSRF, e.g. the result of a strong memory effect while scanning over a feature in the RSRF during the ILT tests. Therefore, the smoothing spline was allowed to be less strict in this region following the shape of the knots.

5.4.4 RSRF calibration sources

The calibration sources were selected to cover a wide diversity in spectral types. This allowed the avoidance of biases to spectral features typical for different spectral classes. The RSRF used in the processing of the ISO Data Archive (OLP Version 10.1) has been corrected using the stars in Table 5.1. For the shortest wavelength section (

4 $\mu$ m and band 5.3-6 $\mu$ m)) we used synthetic spectra based on MARCS models by Decin 2000, [4]. For bands 2A and 2C only sources with spectral type G9 and earlier were used. For the long-wavelength section, composites by Cohen et al. 1992a, [2] were used. Composites are pieces of synthetic spectra and real data spliced to photometric points.

Due to a lack of suitable observations (i.e. a decent S/N) of calibration targets with a well known energy distribution in the region 30-45 $\mu$ m, no correction was applied on the RSRF for band 4.

**Table 5.1:** *The calibration sources used for the correction of the RSRF in OLP Version 10.1, the version of the ISO data reduction pipeline used for the ISO Data Archive.*
Source	HR	Spectral type	Wavelength range [ $\mu$ m]
$\alpha$ Lyr	HR 7001	A0V	2.3 - 30
$\alpha$ CMa	HR 2491	A1V	2.3 - 30
$\beta$ Leo	HR 4534	A3 V	2.3 - 4
$\alpha$ Car	HR 2326	F0 II	2.3 - 12
$\alpha$ Cen A	HR 5459	G2 V	2.3 - 30
$\delta$ Dra	HR 7310	G9 III	2.3 - 12
$\alpha$ Boo	HR 5340	K1.5 III	2.3 - 4, 5.5 - 7, 10 - 30
$\xi$ Dra	HR 6688	K2 III	2.3 - 4, 5.5 - 7, 10 - 12
$\beta$ UMi	HR 5563	K4 III	2.3 - 4, 5.5 - 7, 10 - 12
$\gamma$ Dra	HR 6705	K5 III	2.3 - 4, 5.5 - 7, 10 - 30
$\alpha$ Tau	HR 1457	K5 III	2.3 - 4, 5.5 - 7, 10 - 30
HD 149447	HR 6166	K6 III	2.3 - 4, 5.5 - 7, 10 - 12
$\beta$ And	HR 337	M0 III	2.3 - 4, 5.5 - 7, 10 - 30
$\alpha$ Cet	HR 911	M2 III	2.3 - 4, 5.5 - 7, 10 - 30
$\beta$ Peg	HR 8775	M2.5 III	2.3 - 4, 5.5 - 7, 10 - 30

5.4.5 Accuracy of the RSRFs

5.4.5.1 Residues of artifacts in the ILT RSRF

As mentioned in Section 5.4.3, several features in the ILT RSRF of band 2C and one feature in band 3A were understood to be artifacts. Although the RSRFs have been corrected for these features, residues of them can remain in these wavelength regions.

Band 2C:	9-9.3 $\mu$ m
Band 2C:	10.1 $\mu$ m
Band 2C:	11.0 $\mu$ m
Band 3A:	12.3 $\mu$ m

5.4.5.2 Fringing

All spectral bands of the SWS show fringing caused by one or multiple sets of parallel surfaces in the lightpath that act as a Fabry-Pérot system. The most obvious fringe pattern is seen in band 3 where the Fabry-Pérot effect is caused by the BIBIB detectors themselves.

Order selection filters cause fringing in bands 1 and 2. Compared to the fringes in band 3, the situation is less severe - the amplitude is smaller and the fringe frequency higher, close to the wavelength resolution of the SWS in those bands.

The fringes in bands 3 were also observed during the instrument level tests (Section 5.4.1) so they are also present in the RSRF and will be divided out in the final SWS spectra. However, the beam from the source used during the pre-launch measurements filled the slit of the SWS entirely. Therefore the RSRF measured during these tests has a slightly lower spectral resolution than in-orbit observations of point-like sources. That is the reason why the fringes seen in band 3 are sharper in observations of point-like sources than in the RSRF. Slight pointing errors will also result in a wavelength shift of the spectrum observed, so that the fringes can be shifted slightly with respect to the fringes in the RSRF. This will result in large fringe residues in the spectra in bands 3A, 3C, 3D and 3E. Within the OSIA and ISAP packages, interactive processing tools are available to deal with the residual fringes (Kester, Beintema & Lutz 2001, [21]). See also Section 9.7.

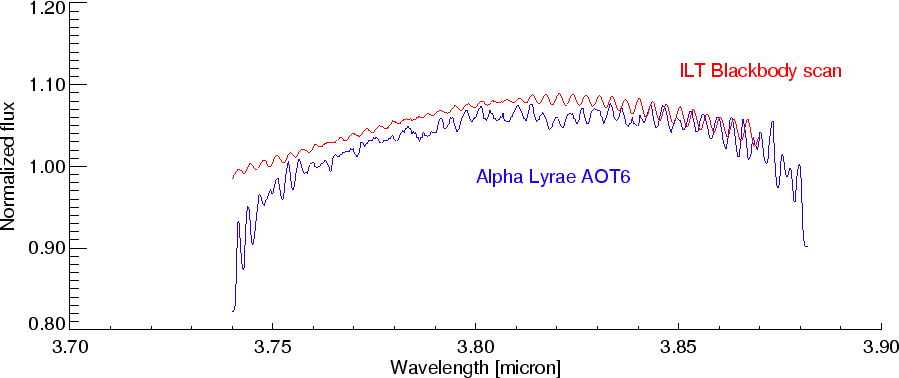
As illustrated in Figure 5.3 the fringes in bands 1 and 2 are hardly resolved in the RSRF while they are completely resolved in high-resolution SWS spectra of stars. This will often limit the S/N that can be achieved with the ISO-SWS at full resolution in those bands.

**Figure 5.3:** *In full-resolution scan SWS06 observations of point-like sources the fringes (here in off-band data band 1D) are better resolved than in the ILT blackbody scans.*
$\resizebox {\textwidth}{!}{\includegraphics{unresolvedfringes.ps}}$

5.4.5.3 Wavelength regions showing order leakage

**Figure 5.4:** *Band 3 data showing the leak around 27 $\mu$ m.*
$\resizebox {13cm}{!}{\includegraphics{leak.eps}}$

The wavelength range of the SWS grating section extends over several octaves. A set of dichroic beamsplitters and order selection filters are therefore needed to avoid light from other wavelengths to leak in via lower or higher spectral orders. The order selection filters in the light path of band 3D do not cut off the shorter wavelengths efficiently enough. Band 3D therefore shows leakage from the wavelength region around 14 $\mu$ m. Typically about 10% of the flux at 14 $\mu$ m will leak to the 28 $\mu$ m region. The RSRF for band 3D is appropriate for sources that have a relatively low flux at 14 $\mu$ m compared to 28 $\mu$ m and hence show no leakage. In spectra of blue sources a false rise at the end of band 3D is seen (Figure 5.4).

Within the OSIA package the RSRF calibration for bands 4A, 4C and 4D is available. These bands contain the data recorded in the band 4 detectors during the scans of bands 3A, 3C and 3D. From the SWS block diagram (see Figure 2.4), it can be seen that there is no order selection filter in the re-imaging optics of the band 4 detectors. For band 4C, this results in very severe leakage from longer wavelengths. Since stellar spectra were used for the RSRF correction, the impact on the RSRF accuracy is minimal. The primary use of this serendipity data is to verify the strength of spectral features in spectra where the band 3 data is problematic due to fringing. In that case one will typically normalise the continuum measured in band 4 to the continuum measured in band 3. The lower sensitivity with respect to band 3 can also be used in the few cases where the SWS observed high flux sources that (partially) saturated the band 3 detectors.

5.4.5.4 The RSRF for band 4

No in-orbit correction of the band 4 RSRF has been applied due to lack of suitable observations/sources. So the RSRF in band 4 is completely based on laboratory measurement using a very bright, extended source. It is known that the laboratory measurements show a strong de-biasing effect, and it can thus be expected that the shape of the current band 4 RSRF has a global inaccuracy of about 10%.

5.4.5.5 Propagation of RSRF features to the spectra after wrong dark subtraction

The effect on the final spectrum of subtracting a wrong dark-current value depends on the RSRF in the wavelength region affected. The SWS RSRFs are not flat at all. They show steep slopes at the ends of the bands, and various bands show distinct features in their RSRF. The dark current subtraction has to be done properly for a proper RSRF correction.

Dividing poorly dark subtracted data by the RSRF will induce false shapes in regions where the RSRF shows features or where the RSRF has a steep slope. Poor matches between different bands can often be understood (and corrected for) from such a combination of dark current uncertainties and a steep RSRF in the overlap region.

The figures in the next sections show where the RSRF is steep or shows features and thus where the risk for these artifacts exists. If the signal level of a scan is of similar strength as the dark currents for that band, it is wise to check if discontinuities at band overlaps or features whose position coincides with RSRF features are real or artifacts.

5.4.6 Overview of the RSRF curves

In Figures 5.5 to 5.19 we give an overview of the RSRF for one representative detector in each band. The curve plotted below the RSRF is an empirically determined uncertainty on the broadband shape of the RSRF. These uncertainties were determined by examining a large set of observations processed with the appropriate RSRFs (presented in this section) and compared them to the expected spectrum. As such, they do not contain a formal error, but rather an indication of the regions in the RSRFs which are known to be less reliable than other regions. The places where small-scale corrections to the ILT RSRFs were applied can be recognized by a sudden rise in the uncertainty.

**Figure 5.5:** The RSRF for band 1A. The upper panel shows the RSRF while the lower panel displays the relative uncertainty in percent. The red lines indicate the valid wavelength range and the blue bar indicates the key wavelength plus passband.
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_1A.ps}}$

**Figure 5.6:** *The RSRF for band 1B. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_1B.ps}}$

**Figure 5.7:** *The RSRF for band 1D. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_1D.ps}}$

**Figure 5.8:** *The RSRF for band 1E. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_1E.ps}}$

**Figure 5.9:** *The RSRF for band 2A. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_2A.ps}}$

**Figure 5.10:** *The RSRF for band 2B. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_2B.ps}}$

**Figure 5.11:** *The RSRF for band 2C. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_2C.ps}}$

**Figure 5.12:** *The RSRF for band 3A. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_3A.ps}}$

**Figure 5.13:** *The RSRF for band 4A. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_4A.ps}}$

**Figure 5.14:** *The RSRF for band 3C. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_3C.ps}}$

**Figure 5.15:** *The RSRF for band 4C. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_4C.ps}}$

**Figure 5.16:** *The RSRF for band 3D. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_3D.ps}}$

**Figure 5.17:** *The RSRF for band 4D. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_4D.ps}}$

**Figure 5.18:** *The RSRF for band 3E. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_3E.ps}}$

**Figure 5.19:** *The RSRF for band 4. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_4.ps}}$

5.4.7 Fabry-Pérot RSRF

The Fabry-Pérot sensitivity was characterized in instrument levels tests by doing measurements on a calibrated blackbody source within the test cryostat. Figures 5.20, 5.21, 5.22, 5.23 and 5.24 show the SWS Fabry-Pérot spectral response functions.

The spectral response curve has structure on various wavelength scales. Large scale trends are determined by the counteracting effects of increasing detector spectral response with wavelength (until close to the detector cut-off wavelength) and decreasing transmission of the Fabry-Pérot interferometer. Structures on scales of microns or tenths of microns can be traced to the detector spectral response curves and filter transmission curves. A rapid low-amplitude modulation in the 11.4-16 $\mu$ m range is caused by reflections between the surfaces of the transmission filter used behind slit 1 in the long-wavelength section of SWS. This `parasitic Fabry-Pérot' effect is also observed for grating data using the same slit. The stronger modulation detected at $\lambda\geq$ 40 $\mu$ m in the long-wavelength extended range is again caused by a parasitic Fabry-Pérot effect, this time in a reflecting

filter. The nearby `reststrahlen' resonance of

causes strong variations with wavelength of the indices of refraction and absorption, leading to the observed modulation pattern. The modulations were characterized with sufficient accuracy to allow good flux calibration in the extended wavelength ranges.

**Figure 5.20:** *The RSRF for band 5A. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_5A.ps}}$

**Figure 5.21:** *The RSRF for band 5B. See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_5B.ps}}$

**Figure 5.22:** *The RSRF for band 5C See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_5C.ps}}$

**Figure 5.23:** *The RSRF for band 5D See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_5D.ps}}$

**Figure 5.24:** *The RSRF for band 6 See Figure 5.5 for explanation.*
$\resizebox {12cm}{!}{\includegraphics{rsrf_overview_6.ps}}$

5.4.7.1 Diffraction losses

The SWS Fabry-Pérot sub-instrument suffers from diffraction losses caused by the fact that the aperture is comparable in size to the ISO diffraction disk. The effect of these diffraction losses is however not large, and Figure 5.25 shows it as a function of wavelength.

**Figure 5.25:** *Computed ISO diffraction losses for the SWS Fabry-Pérot channels. The fraction of the ISO diffraction disk accepted by the effective SWS Fabry-Pérot aperture is shown as a function of wavelength.*
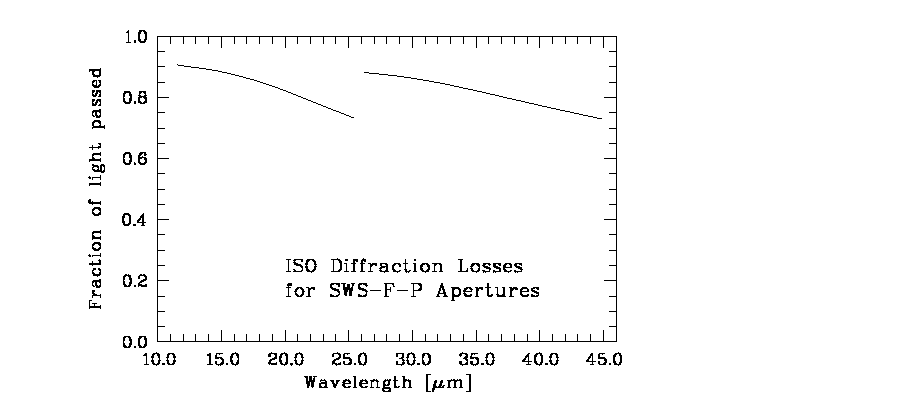
$\rotatebox {-90}{\resizebox{!}{12cm}{\includegraphics{5_11.eps}}}$

5.4.7.2 Leakage in the Fabry-Pérot

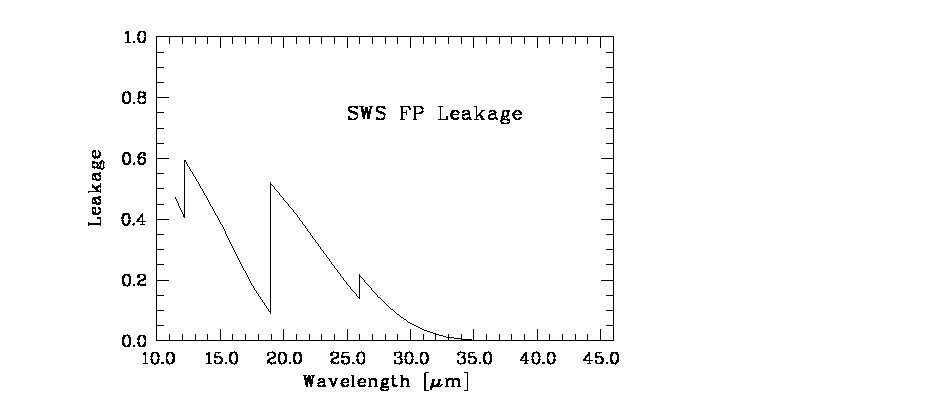
The Fabry-Pérot section uses the grating as an order selector that suppresses unwanted FP orders. This suppression is not complete for part of the SWS wavelength range. Neighbouring FP orders `leak' through the wings of the grating instrumental profile, contributing significantly to the total measured signal (See Figure 5.27). For observations of a single line superposed on a smooth continuum, the only drawback of leakage is a more complicated flux calibration, since leakage will increase the observed continuum but not the line. More serious effects occur in crowded spectra, where strong lines seen in the `wrong' FP order may significantly distort the observed spectrum, requiring observations of wider wavelength ranges in order to determine the severity of this effect and `clean' the spectrum.

Leakage has been quantified by analysis of the grating instrumental profile as seen by the FP detectors in scans of solid state laser lines. Figure 5.26 shows the leakage as a function of wavelength. This figure must be used with caution, since it is based on extrapolating the grating instrumental profile from measurements at only a few wavelengths of laser lines.

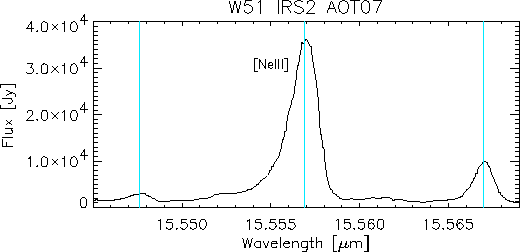
Figure 5.27 shows the effect of leakage on a observation of a single line specially planned to observe the leakage. Because the observation was carried out over a large wavelength interval two `ghost' lines appear either side of the real line. Usually these `ghost' lines would not appear in observations, as they cover a much smaller wavelength range. The observed NeIII line is very strong and, as the FP scans from longer to shorter wavelengths, the line appears non-symmetric because of memory effects in the Si:Sb detector. The 2 leaking orders do not have the same intensity because the grating instrumental profile is not centred on the main order. This slight deficiency in the grating wavelength calibration, although within specifications, translates into the non-symmetric pattern.

The spectral response data in Section 5.4.7 have not been corrected for the effects of leakage, i.e. they refer to the total signal.

**Figure 5.26:** SWS Fabry-Pérot leakage. Leakage is defined here as the fraction of the total detected signal that originates in unwanted Fabry-Pérot orders. The data shown here are based on extrapolation from measurements at a few wavelengths.
$\rotatebox {-90}{\resizebox{!}{12cm}{\includegraphics{5_13.eps}}}$

**Figure 5.27:** Example of FP leakage on a single line. A large wavelength range was scanned for this measurement, resulting in two `ghost' lines at approximately 15.548 and 15.567 $\mu$ m from leakage of the real line at 15.557 $\mu$ m.
$\resizebox {12cm}{!}{\includegraphics{fp_leakage.eps}}$

5.4 The Relative Spectral Response Function (RSRF)