The band 2 (Si:Ga), 4 (Ge:Be), 5 (Si:Ga) and 6 (Ge:Be) detectors used in SWS `remember' their previous illumination history. Going from low illumination to high illumination, or vice versa, results in the detectors asymptotically reaching their new output value. These are referred to as memory effects or transients. Bands 1 (InSb) and 3 (Si:As BIBIB) are not affected by memory effects due to the different detector material used.

Figure 9.1 gives an example from all bands during illumination changes. In this figure it can be seen that bands 2, 4, 5 and 6 have severe memory effects, while bands 1 and 3 show no such effects - these detectors instantaneously reach the signal level corresponding to the new illumination levels.

**Figure 9.1:** *The SPD output of all bands during illumination changes, showing memory effects in bands 2, 4 5 and 6 but none in bands 1 and 3.*
$\resizebox {12cm}{!}{\includegraphics{memory_do.ps}}$

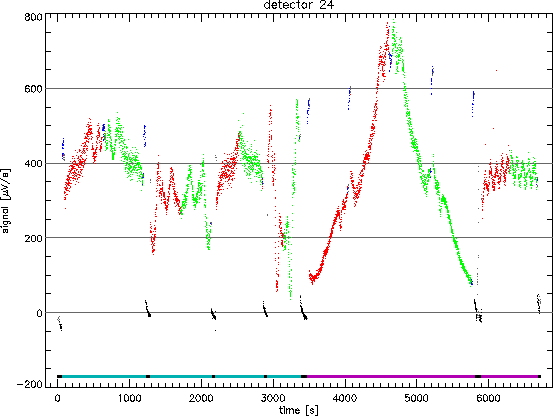
Another example of memory effects is the effect seen in up-down scans of fairly bright sources. For sources with fluxes greater than about 100 Jy memory effects cause the up and down scans in the SPD to differ in response by up to 20% in bands 2 and 4. This effect can be seen in Figure 9.2 for band 2 and in the Figures 9.5 and 9.6 for band 4. Figure 9.2 shows the output of detector 24 against time. Several up-down scans were taken during this measurement, interspersed with dark currents and sometimes reference scans. During a reference scan the grating is moved to a fixed wavelength position to (re)measure the same flux level. This was done to obtain more information on the memory effects, although the scans were never explicitly used for this purpose. The up-down scans have a clear asymmetric shape, the dark currents are not constant and the reference scan do not yield the same flux levels. All this is indicative of serious memory effects.

**Figure 9.2:** Example of memory effects in band 2 on up-down scans as seen in an SPD of an SWS06. The up and down scans are colour-coded differently: red for the up-scan and green for the down-scan. The so-called `reference scans' are in blue (see Section 3.2.2 for further discussion). At the bottom is a bar indicating the aperture used: aperture 2 in mint, aperture 3 in purple and black for aperture closed. The asymmetry in up and down scan is evident. Also the reference scans should be at the same flux level (per aperture setting), which obviously they are not.
$\rotatebox {90}{\resizebox{!}{14cm}{\includegraphics{spd-refmem.ps}}}$

Currently the only memory effects corrected for in the pipeline are those that affect band 2 detectors. They are modelled as changing dark currents. This is mainly discussed in Section 9.2.1. Section 5.3 discusses the general methods used in the dark current subtraction and Section 7.3.3.2 discusses its implementation.

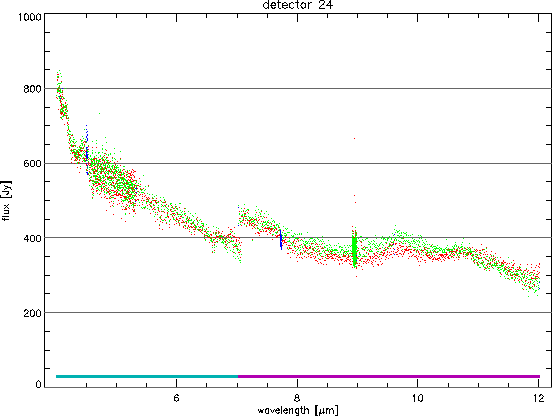
Figure 9.3 shows the result of this in an AAR after application of the transients models described in Section 9.2.1. The up and the down scans overlap quite well and the reference scans find their proper place in the spectrum at 4.5 $\mu$ m and 7.7 $\mu$ m.

**Figure 9.3:** *Example of the result of memory correction in band 2 as seen in an AAR of an SWS06. The colours are the same as in Figure 9.2.*
$\rotatebox {90}{\resizebox{!}{14cm}{\includegraphics{aar-refmem.ps}}}$

For transient effects in the longer wavelengths detectors (band 4 and both FP bands) see Section 9.2.2.

9.2.1 Band 2

An adapted version of the Fouks-Schubert model (Fouks and Schubert 1995, [10]) was developed by Do Kester and successfully implemented in the SWS pipeline to correct band 2 data for transient effects. The method brings the errors (of sometimes up to 20%) down to the few percent level.

The Fouks-Schubert model is written for semi-stationary fluxes, where the semi-part reflects the fact that the detectors do not have to be in an equilibrium state when the next flux step takes place. For a spectrometer like SWS the flux changes continuously, with every reset interval, or even every step of the grating scanner, giving a new constant flux level. The detectors are (almost) never in an equilibrium state but that is taken into account in the formula. The original Fouks-Schubert formula was therefore rewritten into a form more suitable for SWS.

$\displaystyle \alpha _{k} = \frac{ ( 1 - \beta ) \alpha_{k-1} S^{\infty}_{k} } ... ...( 1 - \beta ) S^{\infty}_{k} ) \exp( -\Lambda \beta S^{\infty}_{k} \Delta t ) }$

(9.2)

Here $S_{k}$ is the signal through the detector at time

, $S^{\infty}_{k}$ is the relaxed signal at time $t = \infty$ . It is proportional to the incoming flux. $\beta$ is a constant, to be estimated from the data, and $\alpha_{k}$ comprises the memory effects. $\alpha_{k}$ is dependent on its previous value, $\alpha_{k-1}$ , on the present relaxed signal, $S^{\infty}_{k}$ , and on the constants $\beta$ and $\Lambda$ . $\Delta t$ is the duration of the time step from

. The signal is related to the relaxed signal (or flux) via a constant gain $\beta$ and a changing dark current $\alpha$ . It is a fortuitous coincidence that we used this gain and dark model already in the pipeline. We can identify the product of $\beta S^{\infty}_{k}$ with the incoming flux as it better reflects our present dark current model of signal = flux + dark. The absorption of the constant factor, $\beta$ , in the subsequent calculations is trivial.

When the incoming flux is zero, i.e. when measuring with a closed shutter (a `dark current measurement'), the above expression for $\alpha$ breaks down yielding 0/0. Using l'Hôpital's rule we find a new expression for $\alpha$ when $S^{\infty}_{k}=0$ :

This expression decays to zero in a more or less hyperbolic manner as observed in the Si:Ga detectors. The constant $\beta$ is the fraction of the relaxed signal which expresses itself immediately, so $\beta$ is between 0 and 1. The incoming flux is always positive or zero in case of a dark current. It follows from Equation 9.2 that the values of $\alpha$ are always positive and so is the signal S. We measure, however, (dark) values which are negative for some detectors. So we must conclude that the model is not yet complete, as the zero level in the data cannot be mapped directly on the zero of the model. This is not so disturbing as the zero in the data can be changed somewhat arbitrarily by changing, for instance, the value of `midbit'. Also the zero level shifts when the gain setting changes or when the length of the reset interval changes. All these stepwise zero shifts are artificial in the above sense.

Determining the zero-level function (ZLF) was difficult, as the behaviour at low fluxes is extremely sensitive to the zero level. Piecewise linear functions between dark currents of the same gain setting were used. In this way, the Fouks-Schubert model at low fluxes behaves similarly to the standard dark current subtraction used in all previous pipeline versions, which was deemed correct at low fluxes.

9.2.1.1 Parameter estimation

Now we have a (forward) function which relates the measured signal to the incoming flux in a complicated, non-linear fashion. We only have to invert the relationship, and as the constant $\beta$ is quite large ( $\approx$ 0.8) we can do the inversion iteratively

where $\alpha_{k}$ is calculated with the values of $S^{\infty}_{k}$ from the previous iteration. For most observations the flux stabilises after half a dozen iterations.

In total we have $3 + N_{Z}$ parameters: $\beta$ , $\Lambda$ , $\alpha_{0}$ plus the parameters needed in the ZLF. $\alpha_{0}$ is the value of $\alpha$ before the observation started. The first two parameters are material constants, i.e. they might be fixed over the mission and if that is the case they would have to be estimated only once. The others are related to the flux history in some sense. As this history is unknown these parameters have to be estimated for each observation separately. Note however that the ZLF is chosen to be linear. Consequently for each choice of $\beta$ , $\Lambda$ and $\alpha_0$ the ZLF-parameters can be estimated directly, simplifying the non-linear search for the other parameters. All parameters, however, have to be estimated at least once.

To estimate the parameters we use the redundancy in each observation: up-down and 12 detectors covering more or less the same spectral area. The procedure is described in Kester 2001, [22], or García-Lario et al. 2001, [11].

9.2.1.2 Detector constants

The parameters can be estimated properly when an SPD is used with sufficient dynamic range between 100 and 5000 $\mu$ V/s. For fluxes much larger than 5000 $\mu$ V/s, other memory effects than the ones we are modelling become important. On the other hand when the flux range is too small ( $<100\mu$ V/s) not enough memory effects are present to allow proper extraction of parameters. In that case it is possible, by keeping the parameters $\beta$ and $\Lambda$ fixed and fitting the others, to get proper transients, which will not be much different from the dark current the pipeline would yield.

**Figure 9.4:** In the upper panel: black is the data, green is an estimated input flux, red is the contribution of the memory model, blue is the virtual zero level and yellow is the sum of the input flux (green) and the memory model (red). It can be compared directly to the actual data (black). In the lower panel: black is the residuals, the difference between black and yellow, above. Green is the weights of the data points to be read on the red scale (on the right) and red is the uncertainty in the memory model also on the red scale.
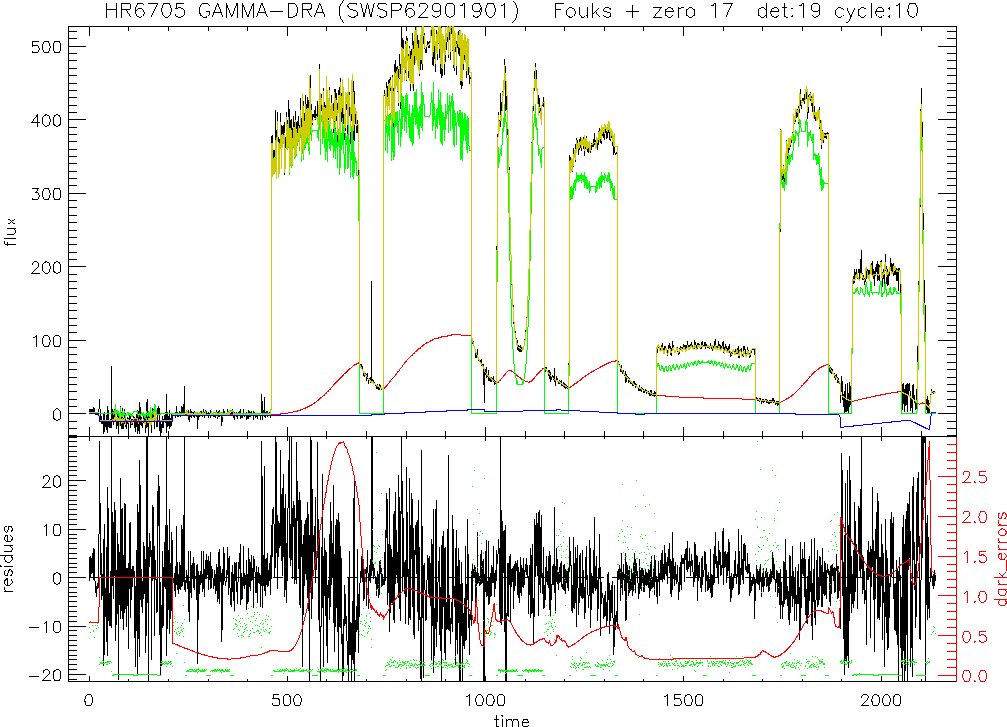$\resizebox {\hsize}{!} {\rotatebox{90}{\includegraphics{DK_gamDra_19.ps}}}$

Figure 9.4 shows an example how the memory model changes over time for one detector during an observation of the calibration star $\gamma$ Dra. In the upper panel the measured data is plotted in black, the relaxed signal in green (symmetric in up-down), the transients, $\alpha_k$ , in red and the zero level in blue. Note that the measured data go below zero and that consequently the model zero level is also below zero. In yellow the model data (relaxed signal + dark) is plotted. They are compared to the true data to calculate $\chi^{2}$ . The memory model has some real impact whenever the flux is more than a few 100 $\mu$ V/s, e.g. between time 500 and 1000. On the other hand when the flux is below 100 $\mu$ V/s, e.g. around time 1500, a straight line between the surrounding dark currents is equally good. In the lower panel the residues are plotted in black, the weights of the points in green (scale on the right). There are some systematic effects, but most of the high noise at high flux has to do with the fact that the measured spectrum is fluctuating (or fringing) severely which cannot be properly followed during the rebinning. In red in the lower panel (to be read on the red scale) is a Monte-Carlo estimate of the error in the memory model.

We determined the parameters $\beta$ and $\Lambda$ from 65 observations of $\gamma$ -Dra and checked it afterward on all SWS01 observations which had a median flux in band 2 higher than 100 $\mu$ V/s. We searched for time variations in the parameters, for variations as function of the flux level and even for variations with temperature, using an extension of the FS formalism. None of the variations was very significant. So we settled for one set of parameters for all of the band 2 detectors, presented in Table 9.1. More details in Kester 2001, [22], or García-Lario et al. 2001, [11].

**Table 9.1:** *Detector constants for transient correction in band 2.*
constant	value
$\beta$	0.82	-
$\Lambda$	63	V $^{-1}$

All pipeline calculations are done with these two parameters fixed. The parameters of the zero-level function and the value for $\alpha_0$ are estimated for each observation separately.

9.2.1.3 Error calculation

When we have arrived at the minimum value for $\chi^2$ the standard deviations and covariance matrix for all parameters is calculated, using a Gaussian approximation at $\chi^{2}_{\min}$ . Typical errors that we find in a good observation are a few per thousand in $\beta$ , a few percent in $\Lambda$ and of the order of 1 $\mu$ V/s in the other parameters ( $\alpha_0$ and the ZLF). However, we are not so much interested in the formal errors in the parameters but much more in the effects they have on the calculated dark current. We use a Monte Carlo scheme where the dark current is calculated 25 times, each time with another randomized set of parameters, drawn from a multidimensional Gaussian distribution representing the full covariance matrix. At each sample the standard deviation of these 25 dark currents is taken as the formal error. See the red line in the lower panel of Figure 9.4.

9.2.2 Memory effects in bands 4, 5 and 6

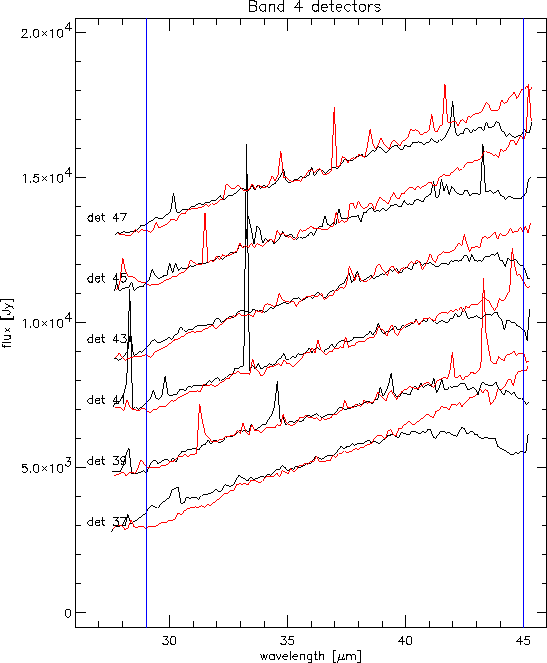
The transient effects in band 4 and in both FP bands can be about as severe as in band 2. Various effects can be seen in Figure 9.5. It is an SWS01 speed 4 observation of K3-50. At the start of the up-down scan (at the longer wavelength side) we see a transient. Some detectors, like 37, display a so-called `hook' effect, some rise faster than others, seeming to get earlier to their relaxed state than the others. At the shorter wavelength there also seems to be some hysteresis effect, where the second part (the down scan in red) seems to stall before getting into the rising mood.

**Figure 9.5:** Example of memory effects in band 4 on an up-down scan as seen in an AAR of an SWS01 speed 4. The scans of the different detectors are offset with respect to each other for clarity. At the start of the upscans (black) at the long wavelength side, various memory effects can be seen, some with so-called `hooks' (dets 37, 45 and maybe 47). The down scans (red, running from short to longer wavelengths) generally show less transient effect. Still there is some systematic difference between up and down scans around 30 $\mu$ m which is probably attributable to transients. Which one of the up or down scans is affected is unclear. The blue lines show the official borders of band 4.
$\resizebox {13cm}{!}{\includegraphics{band4mem-s4.ps}}$

Figure 9.6 displays the same object but then in an SWS01 speed 2 observation, i.e. scanning the spectrum 4 times as fast. It shows the same general trends as in Figure 9.5. In the time domain all detectors react in exactly the same way, which means that in the spectral domain it seems much slower. Both the hook and rise at the start and the hysteresis just after the turning point can be seen. This speed 2 observation has much more glitches; it might have been taken in a more unfavourable part of the orbit. Note that these glitches have their tail, if any, in the time direction, to the left for the up scans (black) and to the right for the down scans (red).

**Figure 9.6:** Example of memory effects in band 4 on an up-down scan as seen in an AAR of an SWS01 speed 2. The same colour coding applies as in Figure 9.5. As this observation is done 4 times as fast as the previous one, the transient effects seem to spread out over a much wider wavelength range.
$\resizebox {13cm}{!}{\includegraphics{band4mem-s2.ps}}$

Unfortunately we do not have a proper model to correct for transients in band 4. The FS model applies only to Si:Ga detectors as only for these detectors the assumptions are valid which simplified the full set of interdependent differential equations that describe transients in general. With these assumptions these equations can be integrated into the closed system which yield the FS model. In the future it might be possible to extend the FS equations with first order corrections, which then might successfully be applied to band 4 detectors too.

For the FP detectors (Si:Sb and Ge:Be) the transients can be as serious as in band 4 (Ge:Be). However due to the fact that the flux levels seen by these detectors are generally quite low, the problem is not as severe as in band 4. This is a fortunate situation as we will never be able to correct for transients because we do not have up-down scans for the FPs. The FP scanners could only be driven in one direction with full paralellisation of the meshes. So transient information and spectral information is inextricably mixed.

9.2.3 Reference scan memory effects

The combined effects of reference scans (described in Section 3.2.2) and detector memory effects produced from band 2 and band 4 detectors during SWS06 observations can be seen in Figure 9.2. Reference scans were introduced to get a handle on the memory effects but as such they were never used due to the lack of an algorithm to do so. Quite early in the mission the number of reference scans per SWS06 was reduced so that only long SWS06 observations had any of them during the up-down scans. They are still present at the beginning and end of an up-down scan. The number was reduced because of the upsetting effect the reference scans had on the rest of the scan.

In band 2 most of the harmful effect of reference scans is removed by the application of the FS model as can be seen in Figure 9.3. In band 4 it just compounds to the transient problems that are already present.

In the document by Leech & Morris 1997, [27], examples of such effects are given and suggestions what to do when they occur^9.1.

9.2.4 Glitch tails

Glitches are caused by such events as fast moving electrons and ions inside the Earth's magnetic field hitting the detectors. Whatever causes a glitch, the effect of one is a sudden change in the output voltage which causes a step (a `glitch') in the affected ramp. Most glitches cause an increase in the output voltage, but some can cause a decrease. For small glitches (the majority) the slopes before and after the glitch are indistinguishable from each other. Figure 2.7 shows an example of a glitch in the 24Hz ERD data in the middle of the second ramp of a measurement.

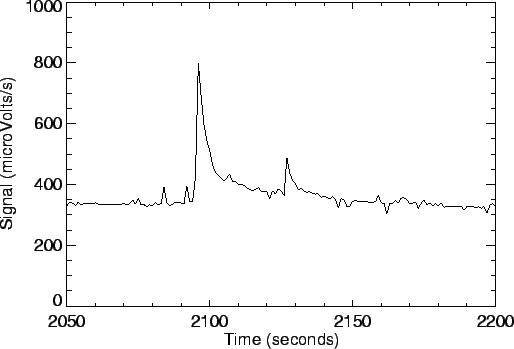
Some glitches, however, are large and have effects that lasts for a long time (they have tails). These tails are especially seen in band 4, due to the detector material and operating conditions, and are probably due to memory effects, see Section 9.2. Figure 9.7 shows two examples of band 4 glitches in the SPD. In both cases the detector requires a long time to stabilise. Note that a strong glitch in one detector can affect other detectors in the same detector array due to cross-talk. More examples of glitches (and tails) can be seen in Figures 9.5 and 9.6. In Figure 9.5 a much rarer negative glitch (with tail) is seen in detector 37 near 42 $\mu$ m.

Both FP bands are even more affected by glitches than band 4. Their detectors are somewhat larger in size and thus catch more cosmic rays. See Figure 9.1.

Derive-SPD attempts to correct for glitches, and for details of how this is accomplished see Section 7.2.8. No attempt is made to correct for tails.

**Figure 9.7:** *Two examples of less-frequent long lasting glitches. The data shown is SPD from a band 4 detector.*
$\resizebox {12cm}{!}{\includegraphics{long-glitch.eps}}$