next up previous contents index
Next: 7.4 Signal Processing: Staring Up: 7. Data Processing Level: Previous: 7.2 Ramp Processing

Subsections


7.3 Signal Processing: Staring PHT-P and PHT-C


7.3.1 Reset interval correction

Detailed description: Section 4.3.3

The detector CRE's give systematically different signals for different reset intervals under constant illumination conditions. Analysis of a photometric measurement requires signal information of other measurements such as internal calibration, background, external calibration, target, etc. If these measurements have not the same readout set-up systematic errors are introduced into the photometric calibration.

It is found that a signal $s(RI,~DAT\_RED)$ obtained with a given reset interval RI and data reduction DAT_RED can be converted to a signal $s(RI_x,~DAT\_RED_x)$ of a different CRE setting according to:


$\displaystyle {s(RI_x,~DAT\_RED_x)\,=\,A^x_0(RI_x,DAT\_RED_x,RI,DAT\_RED)}$
    $\displaystyle + A^x_1(RI_x,DAT\_RED_x,RI,DAT\_RED){\cdot}s(RI,~DAT\_RED)~~~~~~[V/s],$ (7.6)

where $A^x_0$ is the offset value and $A^x_1$ is the slope in the relationship. Both parameters differ for different detectors. The reset interval dependence is corrected for by transforming all signal values $s(RI, DAT\_RED)$ to the corresponding values $s(RI=\frac{1}{4}\,s, DAT\_RED=1)$ of a reference reset interval:


$\displaystyle {s(RI=\frac{1}{4}~s,~DAT\_RED=1)\,=\,A_0(RI,~DAT\_RED)}$
    $\displaystyle + A_1(RI,~DAT\_RED){\cdot}s(RI,~DAT\_RED)~~~~~~{\rm [V/s]},$ (7.7)

where the superscripts and subscripts $x$ have been dropped to indicate that the constants $A_0$ and $A_1$ only refer to the reference reset interval with DAT_RED=1.

Ancillary data required:

For each detector the correction factors $A_0$ and $A_1$ are stored in Cal-G files PP1RESETI, PP2RESETI, and PP3RESETI for the P detectors and PC1RESETI and PC2RESETI for the C detectors (Section 14.6). There is no reset interval correction for PHT-S measurements.


7.3.2 Dark signal subtraction

Detailed description: Section 4.2.6

The dark signal is subtracted from the signal as follows:


\begin{displaymath} s'({\phi}(t)) = s({\phi}(t)) - s_{dark}({\phi}(t)) \end{displaymath} (7.8)

Where $s'({\phi}(t))$, $s({\phi}(t))$, and $s_{dark}({\phi}(t))$, are the corrected, initial, and dark signal, respectively. The orbital phase ${\phi}(t)$ ranges between 0 and 1 where 0 is the moment of perigee passage and 1 is a full revolution later. The ERD contains the keyword TREFPHA2, which is the orbital phase at the start of the measurement. The value for ${\phi}(t)$ in Equation 7.8 corresponds to the time at mid-point of a chopper plateau.

For chopped measurements with PHT-P and PHT-C the dark signal is subtracted from the generic pattern according to Equation 7.8 (Section 7.5). Dark signal subtraction is necessary because the subsequent signal analysis can involve not only the difference signal but also the absolute signal level. In the case of chopped measurements with PHT-S, the dark signal subtraction is not necessary (Section 7.6.4).

Ancillary data required:

Dark signal tables for each detector-pixel combination have been derived from dedicated in-flight observations. The tables contain a value for the dark signal plus uncertainty (in V/s) for each detector pixel as a function of orbital phase. The data are stored in Cal-G files PPDARK (for detectors P1, P2, P3), PC1DARK (for all 9 pixels of C100), PC2DARK (for all 4 pixels of C200), see Section 14.7.


7.3.3 Correction for non-linear detector response of PHT-P and PHT-C

Detailed description: Section 5.2.2

Analysis of measurements of celestial standards showed that the derived values of the detector responsivities (photo-current per incident flux) are not constant. This can be due to gradual responsivity changes of a detector during a revolution independent of incident flux, we call this the time dependent part of the responsivity variation. Variations can also be due to the fact that the detector responsivity is a function of incident flux. This processing step corrects for the latter effect, the signal dependent detector responsivity.

The non-linear behaviour is found to be different for the different filters. The PHT-P and PHT-C photometric calibration scheme uses the internal reference source (FCS) measurements for the derivation of the actual detector responsivity at a given flux level. The inaccuracy due to non-linear detector response is minimized when the in-band powers for the sky and FCS measurement are similar. Large inaccuracies are introduced in case of multi-filter, multi-aperture, and mapping measurements where a large dynamic range in signals has to be calibrated with one FCS signal level. For a detailed description of the signal linearisation see Schulz 1999, [51].

To correct for responsivity non-linearities, a signal correction $H$ is applied such that in measurements of known sources the detector responsivity $R(s)$ becomes constant independent of flux or signal $s_{new}$ (see Section 5.2.5):


\begin{displaymath} s_{new} =\,H^{f,i}(\vert s_{old}\vert), \end{displaymath} (7.9)

where $H$ is not only a function of signal but also of filter $f$ and detector pixel $i$. For the determination of $H$ the time dependent responsivity component was assumed to add only statistical noise to the measurements. In principle $H$ is defined only for positive signals. To make $H$ useful in practice, it is assumed that the correction function goes through the origin (zero) and is point-mirrored in the origin to cope with negative signals.

Ignoring the time dependent component in $R(s)$, the signal linearisation causes the responsivity of a detector to become one value independent of the signal level: $R(s_{new})=R'$. In principle, for the flux calibration, the precise value of $R'$ is arbitrary as long as an FCS measurement is performed close in time, which relates the corrected signal $s_{new}$ to the power on the detector. The signal linearisation tables are derived per filter and are normalised to yield the median of all measured responsivities.

Ancillary data required:

The corrections are stored in Cal-G files P*SLINR.FITS, where (*) stands for P1, P2, P3, C1, and C2, see Section 14.8. These are in essence lookup tables giving the corrected signal for a given input signal per filter and detector pixel. To determine signal values intermediate between the table values, a linear interpolation is applied.


7.3.4 Signal deglitching

Detailed description: Section 4.4

The charges released by a cosmic particle hit cause an effective increase in signal level. Low energetic hits affect only one signal, but high energetic hits can cause several consecutive signals to be higher. A high hit rate can cause the mean signal level in a measurement to increase.

Assuming that the signal distribution is normal on a local scale, a local distribution method is used to filter out signal outliers. The method consists of a `box' sliding along the time axis, defining local distributions as it goes. The maximum and minimum values of the signals are excluded from the calculation of the standard deviation. The exclusion of the extremes in the local distribution makes the deglitching more robust and efficient.

Signals are flagged that are outside a given number of standard deviations from the median for a given local distribution. A signal is eventually discarded in case it is flagged a pre-set number of times. This process is iterated several times.

If the number of available signals is insufficient then a signal is discarded whenever its uncertainty ${\Delta}s(i)$ (Section 7.2.10) is greater than a given threshold. The controlling parameters of the algorithm are given in Table 7.1.


Table 7.1: Parameters for signal deglitching.
Parameter Value Description
min_deglitch 5 minimum points to apply
max_error 1 [V/s] maximum error allowed if number of
    points is less than min_deglitch
n_iter 2 number of iterations of deglitch filter
n_local 20 number of points in local distribution
n_step 1 the number of points to move the `box'
    for the local distribution each time
n_sigma 3 rejection factor: number of standard
    deviations from local median.
n_bad 2 number of times a point has to be flagged
    as `bad' before it is rejected.

The accuracy of this method depends on the glitch frequency and the values of the tuning parameters (Guest 1993, [13]). The number of signals affected by glitches is stored in the header of the SPD product (keyword RAMPDEGL, see Section 13.3.1.3)

Ancillary data required:

None


7.3.5 Transient correction

Detailed description: Section 4.2.3

A routine has been implemented which detects the presence of a significant signal transient on a chopper plateau. When a transient is detected, a range of unreliable signals will be flagged. The algorithm is iterative and is applied until either

It is assumed that a detector transient shows up as a trend which causes either a systematic increase or decrease of the signal level. The signal level will eventually become stable in time when the signal reaches its asymptotic limit. The presence of such a trend is detected by applying the non-parametric Mann statistical test to the signals (e.g. Hartung 1991, [15]). This involves computing a statistic C:


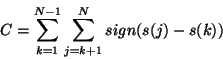\begin{displaymath} C = \sum_{k=1}^{N-1} \sum_{j=k+1}^{N} sign(s(j)-s(k)) \end{displaymath} (7.10)

where,

sign(s(j) - s(k)) = +1 if s(j) $>$ s(k)
  = 0 if s(j) = s(k)
  = -1 if s(j) $<$ s(k)

for all signals s(k), where $k$ = 1,...,N and N is the number of signals on the chopper plateau. The presence of a transient can be detected by comparing C against the corresponding Kendall k-statistic for a given confidence level.

Alternatively, as the number of signals is generally large, it is more convenient to compute the statistic C(*) which can be compared with the quantile of a normal distribution:


\begin{displaymath} {C(*) = \frac{C}{\sqrt{N(N-1)(2N+5)/18}}}~. \end{displaymath} (7.11)

The algorithm requires the following parameters:

The result, $C(*)$, is tested against the null hypothesis which assumes absence of drift. This corresponds to a critical value of $C(*)< 1.645$ for ${\alpha} = 0.05$. A test is made on whether the drift is up ($C(*)< 1.645$) or down ($C(*)>-1.645$).

The algorithm initially performs the test on all available signals on a chopper plateau. If the null hypothesis is rejected, then the test is performed on the second half of the data and the first half is rejected. If the null hypothesis is again rejected, then the second half of the second half is tested etc. The iteration stops either when the null hypothesis is accepted or when there are too few signals (N$\leq$N(min)) to apply the test. Information on the outcome of the procedure is stored per chopper plateau by setting the pixel status flags 2 (`drift fit applied successfully') or 4 (`drift fit may not be accurate') in the SPD records (see Sections 7.12 and 13.3.14).

Since the absolute signal of the FCS measurement determines the responsivity and hence the absolute level of the flux calibration any unstabilised FCS signal has direct impact on the calibration accuracy. For a given observation, the SPD header keyword FCSDRIFT is set to TRUE if the pixel status flag has value 4 in the first FCS measurement of a given detector. The flag is set as soon as a pixel is encountered with pixel status=4.

Ancillary data required:

None


7.3.6 Averaging signals of same instrument set-up

Detailed description: Section 4.2.6

To increase the signal-to-noise ratio, all valid signals on a single chopper plateau are averaged. The following formula is applied:


\begin{displaymath} {\langle s\rangle} = {\frac{\sum_{1}^{N}w_{j}\times s'_{j}} {\sum_{1}^{N}w_{j}}}~~~~~~~~~~[V/s],\\ \end{displaymath} (7.12)

where $N$ is the total number of valid signals on the plateau and $w_{j}=({\Delta}s(j))^{-2}$ is the statistical weight of each signal obtained from its associated statistical uncertainty propagated from the previous signal processing steps. The value of $N$ is stored in the PxxSNSIG field of the SPD record.

The plateau average is either (1) the average of the signals which are not flagged as drifting according to the test described in Section 7.3.5 or (2), if the test fails, the average of the last 7 signals of the plateau or the last 8 s of data, whichever is longer in time.

If it is not possible to calculate a weight for any of the signals on a plateau, then all signals will have a weight $\rm w_{j}$ = 1 assigned. This can happen when the ramps consist of only 2 useful readouts. If no weight can be calculated for a subset of the signals on the plateau, then these will be ignored by setting $\rm w_{j}$ = 0.

The uncertainty of the average signal is derived from the rms of the individual signals:


\begin{displaymath} {\Delta \langle s \rangle = \sqrt{\frac{\sum_{1}^{N}w_{j}\... ...langle s \rangle)^{2}} {(N-1)\sum_{1}^{N}w_{j} }}}~~~~[V/s]. \end{displaymath} (7.13)

Ancillary data required:

None


7.3.7 Obtaining the median of all photo-currents

Detailed description: none

The signal distribution can be non-Gaussian due to signal transients or due to the presence of many positive signal outliers caused by glitches which have not been filtered out completely. In such case, the median signal is a better estimate for the signal per chopper plateau than the average. The median and the quartiles in conjunction with the weighted average should retain information on a non-Gaussian signal distribution. For a gaussian distribution the median is close to the average, and the quartiles fall within the uncertainty interval.

Therefore the median ( ${\rm\langle s(j) \rangle}^M $) and first and third quartile of all available signals are calculated. In contradistinction to the computation of the weighted average, the determination of the median, first, and third quartile values does not exclude signals that are flagged as unreliable by the signal deglitching or transient correction.

For very small signals and ramps with few readouts the quantization by the A/D converter becomes important. The signals in a measurement will have only a discrete number of values. In these cases the median and quartiles are not good estimates.

Ancillary data required:

None


7.3.8 Ramp statistics in SPD and Cal-A headers

Detailed description: none

Useful statistics about readout and signal discarding collected along the signal processing chain is made available to the observer. The statistical information is stored in the SPD product headers.

Ancillary data required:

None

next up previous contents index
Next: 7.4 Signal Processing: Staring Up: 7. Data Processing Level: Previous: 7.2 Ramp Processing
ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc