next up previous contents index
Next: 7.6 Signal Processing: Chopped Up: 7. Data Processing Level: Previous: 7.4 Signal Processing: Staring

Subsections


7.5 Signal Processing: Chopped PHT-P and PHT-C

7.5.1 Processing overview for chopped observations

Detailed description: see also Section 5.2.3

Analysis of many chopped observations performed with PHT-P and PHT-C (involving AOTs PHT03, PHT04, and PHT22) has shown that the `conventional' processing method had to be changed drastically. The main driver for this is that chopped measurements do not give stabilised signals which cause significant losses on the true difference signal. Most of the processing steps which were commonly shared between the staring and chopped observations became obsolete for the chopped observations. Instead, a separate SPD level processing was used.

The present signal derivation relies on the analysis of signals from pairs of consecutive readouts rather than signals per ramp. This gives better statistics of the signals per chopper plateau, since in many chopped measurements each chopper plateau covers only a few (typically 4) ramps.

To increase further the robustness in determining the difference signal, the repeated pattern of off-source and on-source chopper plateaux is converted into a `generic pattern'. The generic pattern consists of only 1 off- and 1 on-source plateau and is generated using an outlier resistant averaging of all plateaux. The shape of the generic pattern determines the correction factors with regard to stabilised staring measurements.

The FCS measurement is used to determine the responsivity of a given observation. The chopped FCS measurements are treated in the same way as the chopped sky measurements, namely for both types of measurement a generic pattern is constructed.

Using a symmetry assumption, the corrected signal level of FCS1 is determined from the measured signal levels of FCS1 and FCS2 and applying the same signal loss correction as for the sky measurements. Following the creation of a generic pattern, the DERIVE_SPD processing proceeds as for staring mode observations from reset interval correction to flux calibration, which uses the corrected FCS1 signal of the chopped FCS measurement.

After reading the ERD the following processing steps are performed for Derive_SPD:

  1. ramp linearisation,
  2. generic pattern creation,
  3. reset interval correction,
  4. dark signal subtraction,
  5. signal linearisation,
  6. determination of the difference signal $s_{s+b}-s_b$ from pattern,
  7. determination of the difference signal corrected for chopped signal losses,
  8. flux calibration.

Steps 2, 6, and 7 are explained in more detail in the following sections.

Ancillary data required:

None

7.5.2 Setting up data for generic pattern construction

Detailed description: none

A chopper unit comprises two consecutive chopper plateaux, in particular either plateaux on the background and source or on FCS2 and FCS1. The number of chopper units $N_u$ and chopper dwell time $t_{dwell}$ of a measurement in a given chopper mode is determined according to:


$\displaystyle N_u$ $\textstyle =$ $\displaystyle \frac{t_m}{2{N_r}{t_r}}~~~~~~{\rm rectangular~and~triangular~mode}$ (7.21)
$\displaystyle N_u$ $\textstyle =$ $\displaystyle \frac{2t_m}{3{N_r}{t_r}}~~~~~~{\rm sawtooth~mode}$ (7.22)

and


\begin{displaymath} t_{dwell} = {N_r}{t_r} = 2^{(n_d-1)}, \end{displaymath} (7.23)

where:

In rectangular mode one full chopper cycle corresponds to one chopper unit:


\begin{displaymath} unit = background + source, \end{displaymath} (7.24)

in triangular mode one chopper cycle corresponds to two consecutive chopper units:


$\displaystyle 1^{st}~unit$ $\textstyle =$ $\displaystyle background~1 + source,$ (7.25)
$\displaystyle 2^{nd}~unit$ $\textstyle =$ $\displaystyle background~2 + source,$ (7.26)

and in sawtooth mode, one chopper cycle ( $background~1\,{\Rightarrow}\,source\,{\Rightarrow}\,background~2$) also corresponds to two consecutive chopper units, but the last plateau of the second unit is regarded as missing and filled up with zeros:


$\displaystyle 1^{st} unit$ $\textstyle =$ $\displaystyle background 1 + source,$ (7.27)
$\displaystyle 2^{nd} unit$ $\textstyle =$ $\displaystyle background 2.$ (7.28)

The time interval of a logical ramp is defined as 1/8 of the duration of a chopper unit and can be derived from:


\begin{displaymath} N_{read} = \frac{(NDR+1)N'_r}{4} \end{displaymath} (7.29)

where:

Before the signal derivation, readouts which can cause systematic deviations are `cleaned' or flagged `bad':

For all available pairs of consecutive readouts the difference signal $s_{diff}$ is computed:


\begin{displaymath} s_{diff} = \frac{V_{i+1}-V_{i}}{t_{i+1}-t_{i}} \end{displaymath} (7.30)

where $V_{i}$ and $V_{i+1}$ in V are the voltages and $t_{i}$ and $t_{i+1}$ are the times of consecutive readouts. Note that the time difference ( ${\Delta}t={t_{i+1}-t_{i}}$) is always the same for a given measurement. After calculation, each $s_{diff}$ is stored in an array in which each element represents a logical ramp in the measurement. In total there are $8{\times}N_u$ elements in this array. In case of sawtooth chopper mode, the array elements belonging to the logical ramps of the second plateau of the even chopper units (2, 4, 6, ...) are set to zero.

Ancillary data required:

None


7.5.3 Generic pattern construction

Detailed description: Section 5.2.3 for an overview

The generic pattern is constructed by stacking the chopper units onto one single unit. However, long term transients or detector drifts which usually last longer than several consecutive chopper units introduce an unwanted noise in the generic pattern. Therefore, before stacking the chopper units, the measurement is corrected for a drift by normalising the chopper units $u$ ($u$=1, 2, 3,...,$N_u$):


Rectangular chop mode:
$\diamond$ compute the median of $s_{diff}$ per chopper unit $u$: $m(u)$
$\diamond$ compute $s'_{diff} = s_{diff}(u)/m(u)$
$\diamond$ store $m(u)$ in an array with $N_u$ elements
$\diamond$ determine a scaling factor $\overline{m(u)}$ from the average over elements $N_u/2$ to $N_u$.


Triangular chop mode:
$\diamond$ compute the median of $s_{diff}$ in two consecutive chopper units $u, u+1$: $m(u,\,u+1)$, ($u$ is odd)
$\diamond$ compute $s'_{diff} =s_{diff}(u,\,u+1)/m(u,\,u+1)$
$\diamond$ store $m(u,\,u+1)$ in an array with $N_u/2$ elements
$\diamond$ determine a scaling factor $\overline{m(u)}$ from the average over elements $N_u/4$ to $N_u/2$.


Sawtooth chop mode:
$\diamond$ compute the median of $s_{diff}$ of the first of every two consecutive units $u, u+1$: $m(u)$, ($u$ is odd)
$\diamond$ compute $s'_{diff} =s_{diff}(u,\,u+1)/m(u)$
$\diamond$ store $m(u)$ in an array with $N_u/2$ elements
$\diamond$ determine a scaling factor $\overline{m(u)}$ from the average over elements $N_u/4$ to $N_u/2$.

 
Before the generic pattern is created two intermediate patterns are obtained by stacking of the $n=$odd (pattern 1) and $n=$even (pattern 2) chopper units. The 8 average signals plus their associated uncertainties which correspond to the 8 logical ramps in each pattern are obtained by computing an outlier resistant mean of the values of $s'_{diff}$ for each logical ramp. For triangular mode the two patterns correspond to the different background positions. For the sawtooth mode, $s'_{diff}$ of the logical ramps 5 to 8 of the even chopper units (pattern 2) is always zero.

The generic pattern for rectangular and triangular chop mode is determined from:

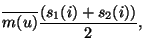$\displaystyle s(i)$ $\textstyle =$ $\displaystyle \overline{m(u)}\frac{(s_1(i) + s_2(i))}{2},$ (7.31)
$\displaystyle {\Delta}1$ $\textstyle =$ $\displaystyle \overline{m(u)}(s_1(i) - s_2(i)),$ (7.32)
$\displaystyle {\Delta}2$ $\textstyle =$ $\displaystyle \overline{m(u)}\sqrt{{\Delta}^2s_1(i) + {\Delta}^2s_2(i)},$ (7.33)
$\displaystyle \Delta{s(i)}$ $\textstyle =$ $\displaystyle max({\Delta}1,{\Delta}2),$ (7.34)

similarly, for sawtooth mode:


$\displaystyle s(i)$ $\textstyle =$ $\displaystyle s_1(i)\overline{m(u)},$ (7.35)
$\displaystyle {\Delta}s(i)$ $\textstyle =$ $\displaystyle {\Delta}s_1(i)\overline{m(u)},$ (7.36)

where:

The 8 signals in the generic pattern are subsequently subject to reset interval correction (Section 7.3.1), dark current subtraction (Section 7.3.2), and signal linearisation (Section 7.3.4).

Ancillary data required:

None


7.5.4 Determination of source signal

Detailed description: none

Based on the generic pattern, the signal of the source $s_{src}$ is determined. The calibration analysis has shown that the appearance of the pattern depends on several parameters such as the detector used, the signal difference, the mean signal level, as well as the chopper dwell time. The determination of the signal $s_{src}$ depends on the detector used:


$\displaystyle {\rm P1:}$ $\textstyle s_{src}\,=$ $\displaystyle med(s(i),\,i=\,5,8\,)-med(s(i),\,i=\,1,4\,)$ (7.37)
$\displaystyle {\rm P2:}$ $\textstyle s_{src}\,=$ $\displaystyle med(s(i),\,i=\,5,8\,)-med(s(i),\,i=\,1,4\,)$ (7.38)
$\displaystyle {\rm P3:}$ $\textstyle s_{src}\,=$ $\displaystyle max(s(i),\,i=\,5,8\,)-min(s(i),\,i=\,1,4\,)$ (7.39)
$\displaystyle {\rm C100:}$ $\textstyle s_{src}\,=$ $\displaystyle ave(s(i),\,i=\,5,8\,)-ave(s(i),\,i=\,1,4\,)$ (7.40)
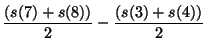$\displaystyle {\rm C200:}$ $\textstyle s_{src}\,=$ $\displaystyle \frac{(s(7)+s(8))}{2}-\frac{(s(3)+s(4))}{2}$ (7.41)

To determine the median, the middle two values of the 4 elements are averaged. Depending on the operation, the signal uncertainties are determined via:

I. In case of average value:

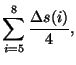$\displaystyle {\rm on~source:}~~~~{\Delta}1$ $\textstyle =$ $\displaystyle \sum_{i=5}^{8}\frac{{\Delta}s(i)}{4},$ (7.42)
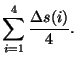$\displaystyle {\rm off~source:}~~~~{\Delta}2$ $\textstyle =$ $\displaystyle \sum_{i=1}^{4}\frac{{\Delta}s(i)}{4}.$ (7.43)

II. For the median value, where $j_1$ and $j_2$ are the indices of the two values averaged to obtain the median:

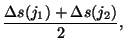$\displaystyle {\rm on~source:}~~~~{\Delta}1$ $\textstyle =$ $\displaystyle \frac{{\Delta}s(j_1)+{\Delta}s(j_2)}{2},$ (7.44)
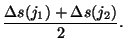$\displaystyle {\rm off~source:}~~~~{\Delta}2$ $\textstyle =$ $\displaystyle \frac{{\Delta}s(j_1)+{\Delta}s(j_2)}{2}.$ (7.45)

III. In case of minimum-maximum value, where $j_1$ and $j_2$ are the indices of the maximum and minimum, respectively:

$\displaystyle {\rm on~source:}~~~~{\Delta}1$ $\textstyle =$ $\displaystyle {\Delta}s(j_1),$ (7.46)
$\displaystyle {\rm off~source:}~~~~{\Delta}2$ $\textstyle =$ $\displaystyle {\Delta}s(j_2).$ (7.47)

Finally, the source signal uncertainty is derived from

\begin{displaymath} {\Delta}s_{src} = \sqrt{{\Delta}1^2+{\Delta}2^2}. \end{displaymath} (7.48)

Ancillary data required:

None


7.5.5 Correction for chopped signal loss: Sky measurement

Detailed description: Section 5.2.3

The source signal $s_{src}$ is corrected for signal loss by the chopper modulation by means of a transformation:


\begin{displaymath} s_{src}^c = \zeta(s_{src},\,det,\,t_{dwell}), \end{displaymath} (7.49)

where $s_{src}^c$ in V/s is the corrected value. The correction function $\zeta$ depends besides $s_{src}$ also on the detector pixel $det$ and chopper dwell time $t_{dwell}$. The function is implemented via look-up tables. Each table gives the correction values for a given detector. Within each table the correction values are ordered by dwell time and detector pixel.

The zero point of $\zeta$ takes care of the vignetting or chopper offset correction (see Section 4.5.3). As a consequence, separate vignetting correction tables are not required.

Assuming that the signal loss is symmetric, i.e. the loss from the on-source signal is gained from the off-source signal, it is possible to correct the on- and off-source signals:


$\displaystyle s_{on}+s_{off}$ $\textstyle =$ $\displaystyle s_{on}^c+s_{off}^c,$ (7.50)
$\displaystyle s_{diff}^c$ $\textstyle =$ $\displaystyle s_{on}^c-s_{off}^c$ (7.51)

then the corrected signals can be determined from:


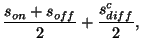$\displaystyle s_{on}^c$ $\textstyle =$ $\displaystyle \frac{s_{on}+s_{off}}{2} + \frac{s_{diff}^c}{2},$ (7.52)
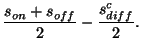$\displaystyle s_{off}^c$ $\textstyle =$ $\displaystyle \frac{s_{on}+s_{off}}{2} - \frac{s_{diff}^c}{2}.$ (7.53)

In practice, the signal loss is asymmetric for detectors P3, C100, and C200. For these detectors the loss on the on-source signal is not equivalent to the gain from the off-source signal. Based on the previous results, the asymmetry is included by using an empirical asymmetry factor $A_{chop}$:


$\displaystyle x$ $\textstyle =$ $\displaystyle 2\vert\frac{s_{diff}}{{s_{on}^c+s_{off}^c}}\vert,$ (7.54)
$\displaystyle A_{chop}$ $\textstyle =$ $\displaystyle A_0 e^{-{\frac{1}{2}}({\frac{x-A_1}{A_2}})^2} + A_3 + A_4 x + A_5 x^2$ (7.55)

where $A_0{\dots}A_5$ are empirical constants with $A_0=\,$0.3558, $A_1=\,-8.129{\cdot}10^{-7}$, $A_2=\,$2.579, $A_3=\,$0.6472, $A_4=\,-1.463{\cdot}10^{-8}$, $A_5\,=~1.285{\cdot}10^{-4}$. Finally, the on- and off-signals corrected for the signal asymmetry are computed for $A_{chop}{\neq}0$ and:
  
If $s_{diff}^c\,>\,0$:

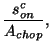$\displaystyle s_{on}^{c*}$ $\textstyle =$ $\displaystyle \frac {s_{on}^c}{A_{chop}},$ (7.56)
$\displaystyle s_{off}^{c*}$ $\textstyle =$ $\displaystyle s_{on}^{c*} - s_{diff}^c.$ (7.57)

If $s_{diff}^c\,{\leq}\,0$:

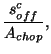$\displaystyle s_{off}^{c*}$ $\textstyle =$ $\displaystyle \frac {s_{off}^c}{A_{chop}},$ (7.58)
$\displaystyle s_{on}^{c*}$ $\textstyle =$ $\displaystyle s_{off}^{c*} + s_{diff}^c.$ (7.59)

In case $A_{chop}\,=\,0$ and for detectors P1 and P2, $s_{off}^{c*}=s_{off}^{c}$ and $s_{on}^{c*}=s_{on}^{c}$.

Ancillary data required:

Cal-G files PP1CHOPSIG, PP2CHOPSIG, PP3CHOPSIG, PC1CHOPSIG, and PC2CHOPSIG contain the look-up tables for $\zeta(s_{src},\,det,\,t_{dwell})$. The description of these files is given in Section 14.10.


7.5.6 Correction for chopped signal loss: FCS measurement

Detailed description: none

For the FCS measurements only rectangular chop mode is used. The generic pattern is constructed in the same way as for the chopped sky measurements for which on-source corresponds to beam deflection to FCS1 and off-source corresponds to FCS2. Adopting the same notation as before but with `on'=FCS1, `off'=FCS2, the same signal loss corrections as presented in Section 7.5.5 apply.

Ancillary data required:

Cal-G files PP1CHOPSIG, PP2CHOPSIG, PP3CHOPSIG, PC1CHOPSIG, and PC2CHOPSIG contain the look-up tables for $\zeta(s_{src},\,det,\,t_{dwell})$. The description of these files is given in Section 14.10.

next up previous contents index
Next: 7.6 Signal Processing: Chopped Up: 7. Data Processing Level: Previous: 7.4 Signal Processing: Staring
ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc