



Next: 5.3 Point Sources Versus
Up: 5. Photometric Calibration
Previous: 5.1 Overview
Subsections
5.2 Calibration Strategy
5.2.1 Calibration involving the FCS
An observation with PHT-P or PHT-C
always includes a photometric reference
measurement using one or both internal fine calibration sources (FCSs, see
also Section 2.7) which are assumed to be stable throughout
the mission. The stability assumption is confirmed by monitoring
measurements against celestial standards throughout the ISO mission.
The emission from an FCS can be changed by adjusting the FCS heating power.
The FCS reference measurement assesses the actual detector responsivity
at the time of the measurement.
The crucial photometric calibration as contained in the Cal-G files
(see Section 5.7.1) is the relationship between heating power
applied to the FCS as commanded by the AOT logic, and the resulting in-band
power received by the detector. This is the basis of the derivation of
the detector responsivity which fixes the relation between signal and
flux for the detector at a given time.
The detector responsivity enables transfer of calibration between
filters of the same detector and/or between apertures.
Transfer of calibration is in practice necessary in case of multi-filter
photometry (PHT03, PHT17/18/19,
PHT22, PHT37/38/39) or multi-aperture
photometry (PHT04) where a single FCS measurement is used
to calibrate combinations of several filters and apertures.
The FCS calibration itself is obtained empirically by comparing the signal
of a designated celestial calibration target and signals of several FCS
measurements. Based on the known spectral energy distribution (SED) of the
calibration target, the known spectral instrument transmissions and
the relative spectral response of the detector, the in-band power is
calculated for each FCS measurement. These in-band powers are then related
to the FCS heating powers via a comparison of the detector signals.
Three types of astronomical targets - all being point sources - have been
used as prime calibrators for the FCSs:
- Stars
Stellar calibrators are most suitable for the 2.5 to 35 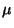 m
wavelength range. The brighter ones can still be extrapolated
reliably out to 300
m
wavelength range. The brighter ones can still be extrapolated
reliably out to 300 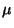 m. A dedicated ground-based preparatory
programme for ISO calibration standards was carried out to provide
the ISO mission with the most consistent and most accurate set of
calibration stars, see Jourdain de Muizon & Habing 1992,
[19],
van der Bliek et al. 1992, [54], and Hammersley
et al. 1998, [14].
Another set of calibrated stellar spectral energy distributions was
provided by M. Cohen from an independent calibration programme
(Cohen et al. 1995, [7]). The
m. A dedicated ground-based preparatory
programme for ISO calibration standards was carried out to provide
the ISO mission with the most consistent and most accurate set of
calibration stars, see Jourdain de Muizon & Habing 1992,
[19],
van der Bliek et al. 1992, [54], and Hammersley
et al. 1998, [14].
Another set of calibrated stellar spectral energy distributions was
provided by M. Cohen from an independent calibration programme
(Cohen et al. 1995, [7]). The 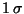 confidence in the absolute calibration of the calibration stars
is about 3% in the 2.5 to 35
confidence in the absolute calibration of the calibration stars
is about 3% in the 2.5 to 35 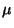 m wavelength range and better than
5-6% at longer wavelengths up to 300
m wavelength range and better than
5-6% at longer wavelengths up to 300 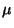 m. The model spectral
energy distribution for Vega (
m. The model spectral
energy distribution for Vega (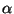 Lyr) has been used to
define the zero point for both programmes.
Lyr) has been used to
define the zero point for both programmes.
- Asteroids
Asteroids are used to cover the 45 to 200 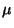 m wavelength range
at intermediate flux levels between bright stars and planets. An
extensive ground and airborne based calibration programme was
carried out to quantify the fluxes and to monitor the light curves
of the prime asteroids 1 Ceres, 2 Pallas, 4 Vesta, and 10 Hygiea,
and other asteroids that have been observed with ISO. For the
current calibration the absolute fluxes of the asteroids
were derived using a thermophysical model (Müller & Lagerros 1998,
[40]). The accuracy of the predicted asteroid
fluxes is in general
m wavelength range
at intermediate flux levels between bright stars and planets. An
extensive ground and airborne based calibration programme was
carried out to quantify the fluxes and to monitor the light curves
of the prime asteroids 1 Ceres, 2 Pallas, 4 Vesta, and 10 Hygiea,
and other asteroids that have been observed with ISO. For the
current calibration the absolute fluxes of the asteroids
were derived using a thermophysical model (Müller & Lagerros 1998,
[40]). The accuracy of the predicted asteroid
fluxes is in general 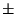 10% in the wavelength range longward of
24
10% in the wavelength range longward of
24 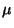 m (Müller & Lagerros 2002, [43])
m (Müller & Lagerros 2002, [43])
- Planets
The outer planets Neptune and Uranus were used for calibration at the
longer wavelengths in the high flux density range up to 1000 Jy. The
model SED's of Uranus at a given time in the mission were derived
from the model by Griffin & Orton 1993, [11]
modified to match the Voyager IRIS data (see `The ISO Handbook:
Vol. III, LWS - The Long Wavelength Spectrometer',
[12]).
Comparison with independent model predictions for Uranus
showed a consistency of better than 10% in the wavelength range
between 30 and 240 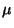 m.
m.
The stability of both FCSs was monitored against the bright secondary
standard NGC6543 as well as against a set of fainter stars.
The ISOPHOT calibration strategy is presented in detail by Klaas et
al. 2001, [28]. A full description of
the ISOPHOT calibration involving the FCS can be found in Schulz
et al. 2002, [53].
5.2.2 Non-linear detector responsivity
Ignoring transient effects (see Section 4.2.3),
the detector responsivity, which is the proportionality between in-band
power and signal, can only be considered as constant under the
following conditions:
- the time between the responsivity measurement and the sky measurement
is short. Over longer time periods the responsivity is a function
of orbital phase and shows a steady increase for detectors
P3, C100, and
C200 as a function of time after curing.
- the signal of the FCS measurement is close to the signal of the sky
measurement. From calibration observations of standard stars it was found
that the detector responsivity depends on the in-band power
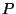 falling onto
the detector
falling onto
the detector
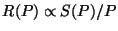 , where the photo-current or signal
, where the photo-current or signal  has a non-linear dependence on power.
has a non-linear dependence on power.
Investigation of the validity of the second condition has shown that
the signal non-linearity can be corrected under the assumption that
the shape of the signal non-linearity function is independent of time.
Since the responsivity is proportional to signal, the responsivity can be
linearised by introducing a linearisation correction 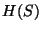 such that:
such that:
where 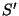 is the linearised signal. Time dependencies, such as the
responsivity dependency on orbital phase, are treated as random scatter.
The correction function
is the linearised signal. Time dependencies, such as the
responsivity dependency on orbital phase, are treated as random scatter.
The correction function 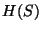 has
been determined empirically from observations of calibration standards.
It is found that
has
been determined empirically from observations of calibration standards.
It is found that 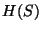 is not only a function of detector, but also
of filter. The determination of
is not only a function of detector, but also
of filter. The determination of 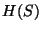 is not straightforward due to the
fact that all measurements of calibration standards include a background
power which is not well known. In addition, time dependent variations of
the responsivity introduces a substantial scatter in the data.
A detailed description is provided by Schulz
1999, [51].
is not straightforward due to the
fact that all measurements of calibration standards include a background
power which is not well known. In addition, time dependent variations of
the responsivity introduces a substantial scatter in the data.
A detailed description is provided by Schulz
1999, [51].
In the photometric calibration of PHT-P and
PHT-C, the signal linearisation
is applied to the mean signal per chopper plateau immediately after
subtraction of the dark signal. In the remainder of this chapter we
assume that the signals 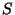 have been linearised unless explicitly
stated.
have been linearised unless explicitly
stated.
5.2.3 Signal correction for chopped observations with PHT-P and -C
The photometric accuracy of chopped observations is completely determined
by losses in the difference signal between the `source+background'
(`on') and `background' (`off') signals. This is caused by detector
transients with time constants greater or equal than the chopper
modulation time (see Section 4.2.3).
Due to these transients the determination of the
difference signal is not trivial. A method was
developed which includes the determination of a generic pattern
for chopped measurements (see Section 7.5).
The signal difference is determined from the generic pattern depending
on the transient behaviour of a given detector - for example, in case
of detector P3
the signal difference is determined from the maximum
of the on-signals and the minimum of the off-signals of the pattern,
and in case of P1 and P2
the median signals of the on- and off-plateaux are used.
This analysis of chopped measurements applied to a sample of calibration
standards yielded an empirical signal correction function 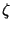 which
corrects a given (linearised) difference signal
which
corrects a given (linearised) difference signal  :
:
![\begin{displaymath}
S_{src}' = \zeta(S_{src},\,det,\,t_{plat})~~~~~~{\rm [V/s]},
\end{displaymath}](img244.gif) |
(5.3) |
where  is the signal corrected for losses due to the
chopper modulation,
is the signal corrected for losses due to the
chopper modulation,  is the detector used, and
is the detector used, and  is the
chopper plateau time (in s). The dependency on
is the
chopper plateau time (in s). The dependency on  and
and  is required to relate the chopper modulation frequency with the
detector specific transient time scales.
is required to relate the chopper modulation frequency with the
detector specific transient time scales.
The AOT PHT32 incorporated the chopper sawtooth mode to
obtain oversampled maps with the PHT-C
detector arrays (Sections 3.5
and 3.10.2).
The movement of the chopper in PHT32 also caused signal transients.
These cannot be corrected with 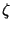 because there is no fixed
on-source and background position as in the pointed chopped observations.
Therefore no corrections are made in OLP for signal losses due to detector
transients in PHT32.
because there is no fixed
on-source and background position as in the pointed chopped observations.
Therefore no corrections are made in OLP for signal losses due to detector
transients in PHT32.
The function 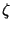 implicitly includes the correction for `chopper
vignetting/offset' (Section 4.5.3) with PHT-C
because the choice of available chopper throws with PHT-C was limited. For
PHT-P the chopper offsets are small. In the case of PHT32 the signals per
chopper plateau are explicitly corrected for chopper offsets:
implicitly includes the correction for `chopper
vignetting/offset' (Section 4.5.3) with PHT-C
because the choice of available chopper throws with PHT-C was limited. For
PHT-P the chopper offsets are small. In the case of PHT32 the signals per
chopper plateau are explicitly corrected for chopper offsets:
![\begin{displaymath}
S' = c_{chop}(f,i,\theta){\times}S~~~~~~~[{\rm V/s}],
\end{displaymath}](img248.gif) |
(5.4) |
where 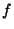 is the filter,
is the filter, 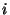 is the detector pixel and
is the detector pixel and  the
chopper deflection with respect to the central field of view. The
input signal
the
chopper deflection with respect to the central field of view. The
input signal 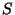 is the total sky signal.
is the total sky signal.
5.2.4 Absolute calibration of FCS
The FCS calibration against celestial standards has been determined for
all 25 PHT-P and
PHT-C
filter bands over the full range of possible astronomical flux densities.
Fluxes were measured of prime calibrators in each available filter band
spanning 3-5 decades of flux range per filter band. For a given calibration
target, the following measurements were obtained in a given filter:
- measurement of the FCS for which zero heating power is applied
(also referred to as `cold FCS measurement' or `FCS straylight
measurement'),
- measurement of one or more background positions,
- measurement of the calibration target, and
- measurement of one to several FCS illumination levels.
The cold FCS measurement provided the zero FCS signal level.
All measurements
of the celestial calibrators included an uncalibrated amount of background
emission which had to be subtracted. The background level was determined by
performing one or more separate background pointings in the same aperture.
For the PHT-C arrays, small raster maps were often used to obtain the
background level during the same measurement.
In the case of multiple FCS measurements, the FCS illumination levels
were tuned such that their in-band powers span a range of about
one decade around the power expected from the calibration target plus
background emission. It is assumed that the responsivity does not depend
on signal in the measured power range (system linearity).
Using the total optical transmission of the instrument and detector
chain (to determine 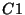 and
and  ) and the source SED, the in-band
power from the calibration source on the detector was computed from
Equation 5.10. By relating the in-band
power of the calibration target to its corresponding signal, the FCS
signals were converted to in-band powers. These are derived for a
measurement in a given aperture in case of PHT-P or for a pixel
in case of PHT-C, according to:
) and the source SED, the in-band
power from the calibration source on the detector was computed from
Equation 5.10. By relating the in-band
power of the calibration target to its corresponding signal, the FCS
signals were converted to in-band powers. These are derived for a
measurement in a given aperture in case of PHT-P or for a pixel
in case of PHT-C, according to:
![\begin{displaymath}
P_{fcs}^f(h) = P^f_{cal}{\cdot}\frac{(S_{fcs}^{f}-S^f_{str})}{S^f_{cal}}
~~~~~~{\rm [W]},
\end{displaymath}](img254.gif) |
(5.5) |
where
 : the in-band power in W for filter
: the in-band power in W for filter 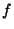 and
FCS heating power
and
FCS heating power 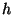 in mW;
in mW; : in-band power in W of the celestial calibrator;
: in-band power in W of the celestial calibrator;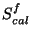 : measured signal in V/s of the prime calibrator after
subtraction of the background signal;
: measured signal in V/s of the prime calibrator after
subtraction of the background signal; : measured FCS signal in V/s;
: measured FCS signal in V/s;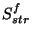 : measured dark FCS signal (straylight) in V/s.
: measured dark FCS signal (straylight) in V/s.
The FCS power calibration tables give the in-band power as a function of
the commanded FCS heating power. It is assumed that the difference signal
between calibration source and background scales linearly with the
difference signal from the FCS measurements. Consequently, the accuracy
of the absolute calibration of the background level depends on
the linearity of the detector from zero to the background level and on the
suppression of parasitic flux, such as straylight. Uncertainties become
higher for flux levels close to the astronomical background because of
the absence of reliable celestial calibrators that are faint.
For PHT-P the tables are normalised to the aperture area, and for
PHT-C the tables refer to the average array. The power falling onto
an individual pixel is derived by for inhomogeneous FCS illumination
(see Section 5.2.5).
The FCS calibration makes the observation independent of long term
responsivity drifts. However, on measurement time scales of order of
32-2048 s, detector transients (Section 4.2.3)
due to flux changes occur and have to be corrected for.
For the determination of the overall FCS calibration drift corrections
have been applied to estimate the signal level of the asymptotic limit.
5.2.5 Photometry with PHT-P and PHT-C
The FCS measurement together with the FCS power calibration tables (see
Section 14.12) are used to determine the detector
responsivity. In the following derivations a separation will be made between
single detector, multi-aperture, and multi-filter subsystems PHT-P and
the multi-filter detector arrays PHT-C.
For a given PHT-P FCS measurement taken with detector  ,
filter
,
filter 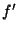 , and aperture
, and aperture 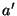 , the responsivity
, the responsivity
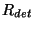 is derived from:
is derived from:
![\begin{displaymath}
R_{det} = \frac{S_{fcs}^{f'}(a')C^{det}_{int}}
{P^{f'}_{fcs}(h)A(a'){\alpha}^{f'}(a'){\chi}^{f'}}
~~~{\rm [A/W]},
\end{displaymath}](img263.gif) |
(5.6) |
For a given PHT-C FCS measurement taken with detector  and filter
and filter
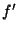 , and for pixel
, and for pixel 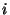 , the responsivity
, the responsivity 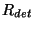 is derived from:
is derived from:
![\begin{displaymath}
R_{det}(i) = \frac{S_{fcs}^{f'}(i)C^{det}_{int}}
{P^{f'}_{fcs}(h){\Gamma}^{f'}(i){\chi}^{f'}(i)}
~~~{\rm [A/W]},
\end{displaymath}](img264.gif) |
(5.7) |
where the prime (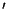 ) indicates the FCS measurement configuration and
) indicates the FCS measurement configuration and
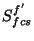 : the signal in V/s from the FCS measurement
in filter
: the signal in V/s from the FCS measurement
in filter 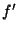 after subtraction of dark signal or FCS straylight
(the latter one is only possible with PHT05 and
PHT25);
after subtraction of dark signal or FCS straylight
(the latter one is only possible with PHT05 and
PHT25);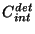 : the integration capacity in A/(V/s) (=farad)
associated with detector
: the integration capacity in A/(V/s) (=farad)
associated with detector  (see Figure 2.5 and
Table 14.5);
(see Figure 2.5 and
Table 14.5);-
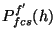 : the in-band power in W for filter
: the in-band power in W for filter 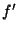 and
FCS heating power
and
FCS heating power 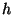 in mW as obtained from the FCS power table, for
PHT-P the power is per mm
in mW as obtained from the FCS power table, for
PHT-P the power is per mm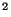 , for PHT-C per pixel;
, for PHT-C per pixel;
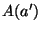 : the area of aperture
: the area of aperture 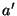 in mm
in mm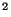 ;
;-
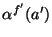 : dimensionless correction for inhomogeneous
illumination of PHT-P aperture
: dimensionless correction for inhomogeneous
illumination of PHT-P aperture 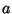 by the FCS in filter band
by the FCS in filter band 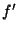 ;
;
-
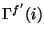 : dimensionless correction for PHT-C pixel
: dimensionless correction for PHT-C pixel 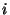 due to inhomogeneous illumination of the array by the FCS;
due to inhomogeneous illumination of the array by the FCS;
-
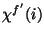 : dimensionless correction for non-uniform
filter-to-filter responsivity of pixel
: dimensionless correction for non-uniform
filter-to-filter responsivity of pixel 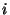 of PHT-C or PHT-P
where
of PHT-C or PHT-P
where 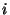 is dropped (single pixel).
is dropped (single pixel).
A few observations have no accompanying FCS measurement which can be
used for the photometric calibration due to e.g. a failure during
the observation or signal saturation. In those cases a default
responsivity is applied which is a fixed value of  corrected for a predictable variation with orbital phase at the time
of the observation.
corrected for a predictable variation with orbital phase at the time
of the observation.
Once the detector responsivity is known, measurements of a celestial source
with filters of the same detector in a multi-filter photometry observation
can be calibrated. For a given PHT-P measurement, the in-band power
 for filter
for filter 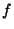 and aperture
and aperture 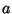 is:
is:
![\begin{displaymath}
P_{src}^{f}(a) = \frac{S_{src}(a)C^{det}_{int}}
{R_{det}{\chi}^{f}}~~~~~{\rm [W]},
\end{displaymath}](img277.gif) |
(5.8) |
For a given PHT-C measurement, the in-band power
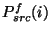 for
filter
for
filter 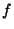 and for pixel
and for pixel 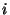 is:
is:
![\begin{displaymath}
P_{src}^{f}(i) = \frac{S_{src}(i)C^{det}_{int}}
{R_{det}{\chi}^{f}(i)}~~~~~{\rm [W]},
\end{displaymath}](img279.gif) |
(5.9) |
where  is the linearised source signal in V/s after dark signal
subtraction. Note that the correction
is the linearised source signal in V/s after dark signal
subtraction. Note that the correction 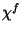 cancels out for a source
measurement taken in the same filter band as for the FCS measurement,
i.e. when
cancels out for a source
measurement taken in the same filter band as for the FCS measurement,
i.e. when 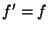 .
To convert from in band power to point source flux density on the sky,
the following relation is used for PHT-P:
.
To convert from in band power to point source flux density on the sky,
the following relation is used for PHT-P:
![\begin{displaymath}
\frac{F_{\nu}^{f}}{k_f} =
\frac{P_{src}^{f}(a)}{C1^f f_{PSF}^{f}(a)}~~~~~{\rm [Jy]},
\end{displaymath}](img282.gif) |
(5.10) |
and for PHT-C5.1:
![\begin{displaymath}
\frac{F_{\nu}^{f}}{k_f} =
\frac{\sum_{i}P_{src}^{f}(i)}{C1^f f_{PSF}^{f}}~~~~~{\rm [Jy]},
\end{displaymath}](img283.gif) |
(5.11) |
where the summation is over all detector pixels 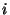 and where:
and where:
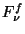 : the source flux density in Jy for an assumed spectral
energy distribution
: the source flux density in Jy for an assumed spectral
energy distribution  = constant;
= constant; : the colour correction, for the spectrum of the observed
celestial source;
: the colour correction, for the spectrum of the observed
celestial source;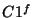 : constant in
: constant in 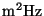 describing5.2 the transmission of the whole optical path for a given filter and
assuming a
describing5.2 the transmission of the whole optical path for a given filter and
assuming a 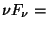 constant reference source spectrum.
The effective size of the primary mirror, reflection losses, filter
transmission, spectral response of the detector, etc. are included;
constant reference source spectrum.
The effective size of the primary mirror, reflection losses, filter
transmission, spectral response of the detector, etc. are included;
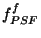 : (dimensionless) fraction of the ISO point spread
function entering the field aperture in case of PHT-P or falling
onto the entire array in case of PHT-C for filter
: (dimensionless) fraction of the ISO point spread
function entering the field aperture in case of PHT-P or falling
onto the entire array in case of PHT-C for filter 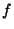 (details can be found in Salama et al. 2001, [47]).
(details can be found in Salama et al. 2001, [47]).
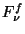 is also referred to as the flux density at the reference
wavelength of the filter band and is the value of the flux density
computed by OLP. It is required that the constant
is also referred to as the flux density at the reference
wavelength of the filter band and is the value of the flux density
computed by OLP. It is required that the constant 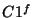 is
identical to the one used in the determination of the FCS power tables.
is
identical to the one used in the determination of the FCS power tables.
5.2.6 Spectro-photometry with PHT-S
At the shortest wavelengths below 10 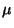 m very high FCS heating powers
are required to obtain a detectable in-band power. Due to the wavelength
coverage of PHT-S no single FCS power can properly illuminate both
SS and SL
arrays without causing saturation in the SL array (a 300 K blackbody
spans 5 orders of magnitude over the wavelength range 2.5-12
m very high FCS heating powers
are required to obtain a detectable in-band power. Due to the wavelength
coverage of PHT-S no single FCS power can properly illuminate both
SS and SL
arrays without causing saturation in the SL array (a 300 K blackbody
spans 5 orders of magnitude over the wavelength range 2.5-12 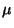 m).
Therefore and due to the fact that the PHT-S detectors turned out to be
very stable, the PHT-S measurements (PHT40) are not accompanied by any
FCS measurement. Without any FCS measurement, the photometric calibration
must be different from that of PHT-P or PHT-C.
m).
Therefore and due to the fact that the PHT-S detectors turned out to be
very stable, the PHT-S measurements (PHT40) are not accompanied by any
FCS measurement. Without any FCS measurement, the photometric calibration
must be different from that of PHT-P or PHT-C.
Monitoring of the PHT-S responsivity at the beginning and end of each
revolution showed that the daily responsivity variation is on average
at most 10% depending on the space weather conditions, see
Section 4.2.5. Shorter time scale responsivity
variations
are mainly due to transient behaviour of the detector responsivity following
an illumination change. The PHT-S transient behaviour is corrected by
applying the calibration method outlined in the remainder of this section.
The PHT-S measurement sequence as provided by the PHT40 AOT has always
the same structure: an initial dark signal measurement of 32s followed
by a sky measurement of 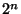 s (
s (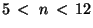 ) either in staring or
chopped mode. This measurement sequence causes the detector to be in a
well defined (dark) state before the illumination by the sky starts.
) either in staring or
chopped mode. This measurement sequence causes the detector to be in a
well defined (dark) state before the illumination by the sky starts.
Due to the long term responsivity stability, the photometric accuracy
of the PHT-S observations is mainly determined by the uncertainties caused
by the responsivity transients
(Schulz 1999, [52]). The photometric calibration of
PHT-S is therefore based on the following assumptions:
- the transient response of an individual pixel depends on
the illumination level.
- the transient response for a given illumination level is
reproducible as long as the flux history is similar.
These assumptions are to a large extent fulfilled by the long term
responsivity stability and the AOT PHT40 design. The only disturbing
parameter is the operational temperature of the detector which affects
the shape of the transient curves. It is, however, found that the
temperature of the detector was quite stable (2.7-3.1K) throughout the
routine phase, i.e. revolution 78 and later. During the Performance
Verification Phase the PHT-S detector temperature was lower (2.4K)
and the calibration methods outlined below are less accurate for
observations obtained in that period.
5.2.6.1 PHT-S staring observations
By observing a large number of calibration stars covering a sufficient
range in flux densities and integration time for each PHT-S pixel, one can
construct an empirical transformation which directly relates the signal
transient 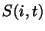 of a given pixel
of a given pixel 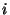 at time
at time 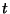 to a flux density
to a flux density
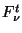 :
:
where  is the transformation and
is the transformation and 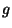 a function which gives the
weight of the correction. We give the flux density a superscript
a function which gives the
weight of the correction. We give the flux density a superscript
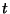 to indicate that the flux itself is supposed to be constant and has
no time dependence. The time resolution is determined by the reset
interval length, i.e. the time between two consecutive signals. This
calibration method is also called `dynamic calibration', because the
spectral response function is adapted to the total brightness and transient
behaviour of each pixel.
to indicate that the flux itself is supposed to be constant and has
no time dependence. The time resolution is determined by the reset
interval length, i.e. the time between two consecutive signals. This
calibration method is also called `dynamic calibration', because the
spectral response function is adapted to the total brightness and transient
behaviour of each pixel.
The weighting function has been introduced to
account for the fact that the transient correction is usually large
on short time scales and close to unity for very long integration
times. It is assumed that the transient signal reaches the long term
detector response asymptotically in time. The final flux 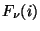 is the weighted average of the transformed signals
is the weighted average of the transformed signals 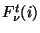 along a
given measurement.
along a
given measurement.
5.2.6.2 PHT-S chopped observations
PHT-S observations in chopped mode have the property that the background
emission (off position) is usually the zodiacal light which is faint at
the PHT-SS wavelengths, and less than 1 Jy at the
longest SL wavelengths.
In addition, the available range in chopper frequencies at low flux
densities is small.
From the analysis of a large range of chopped PHT-S observations of
calibration stars it is found that an accurate photometry can be
accomplished by assuming two calibration components.
One component is the average spectral response function which is the
zero order approximation for the conversion from signal in V/s to flux
density in Jy for each pixel 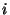 . The second component involves the
correction for flux dependent chopped signal losses due to signal
transients and depends on the difference signal between the on-source
signal and the background off signal:
. The second component involves the
correction for flux dependent chopped signal losses due to signal
transients and depends on the difference signal between the on-source
signal and the background off signal:
![\begin{displaymath}
C^{c,p}(i) = C^{c,p}_{ave}(i) (A_0(i)+
A_1(i){\rm log_{10}}(S_{on}(i)-S_{off}))~~~~~~
{\rm [V\,s^{-1}Jy^{-1}]},
\end{displaymath}](img302.gif) |
(5.14) |
where
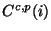 in (V/s)/Jy is the spectral response of pixel
in (V/s)/Jy is the spectral response of pixel 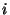 for a point source
for a point source 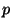 corrected for chopped
corrected for chopped 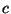 signal loss;
signal loss;-
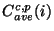 in (V/s)/Jy is the PHT-S average spectral
response function for a point source;
in (V/s)/Jy is the PHT-S average spectral
response function for a point source;
 and
and 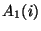 are first order corrections on spectral
response function for chopped measurements depending on the
signal difference;
are first order corrections on spectral
response function for chopped measurements depending on the
signal difference; and
and 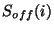 (in V/s) are the on- and off-source
signals.
(in V/s) are the on- and off-source
signals.
The mean spectral response function was obtained by taking the average of
the spectral response functions derived from a number of faint calibration
stars.
5.2.6.3 PHT-S maps
PHT-S maps are obtained by observing a regular grid (raster) by moving
the spacecraft from one grid point to the other. Although the measurement
sequence in PHT40 mapping mode is the same as in staring or chopped mode
(a dark measurement followed by the sky) the assumption of a flux history
similar to that as for the calibration stars is not met for all raster
points in a map except the first one. The photometric calibration is
poorer than for staring or chopped mode observations because only a
`static' response function not correcting for responsivity transients
can be applied. The photometric calibration on each raster point  is
performed by direct conversion of the signal
is
performed by direct conversion of the signal  to a flux
to a flux 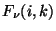 :
:
![\begin{displaymath}
F_{\nu}(i,k) = \frac{S(i,k)}{C^{s,p}_{ave}(i)}~~~~~~{\rm [V\,s^{-1}Jy^{-1}]},
\end{displaymath}](img313.gif) |
(5.15) |
where
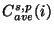 the average spectral response function for PHT-S
staring observations derived from 40 observations of 4 different standard
stars with different brightness.
the average spectral response function for PHT-S
staring observations derived from 40 observations of 4 different standard
stars with different brightness.




Next: 5.3 Point Sources Versus
Up: 5. Photometric Calibration
Previous: 5.1 Overview
ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc
![\begin{displaymath}
P_{fcs}^f(h) = P^f_{cal}{\cdot}\frac{(S_{fcs}^{f}-S^f_{str})}{S^f_{cal}}
~~~~~~{\rm [W]},
\end{displaymath}](img254.gif)
![\begin{displaymath}
R_{det} = \frac{S_{fcs}^{f'}(a')C^{det}_{int}}
{P^{f'}_{fcs}(h)A(a'){\alpha}^{f'}(a'){\chi}^{f'}}
~~~{\rm [A/W]},
\end{displaymath}](img263.gif)
![\begin{displaymath}
R_{det}(i) = \frac{S_{fcs}^{f'}(i)C^{det}_{int}}
{P^{f'}_{fcs}(h){\Gamma}^{f'}(i){\chi}^{f'}(i)}
~~~{\rm [A/W]},
\end{displaymath}](img264.gif)