The image of a perfect point source obtained with a given detector or the footprint of a detector should be known in case one would like to perform:

As part of the PHT calibration programme, extensive mapping of astronomical point sources was carried out in order to determine the footprints of the PHT-SS/SL, C100 and C200 detectors and the PHT-P apertures.

4.5.1.1 PHT-C footprints

The footprints of the C100 detector array pixels were observed at 60 and 105 $\mu$ m (filter bands C_60 and C_105) and of the C200 array at 120 and 200 $\mu$ m. Footprint maps of the four C200 pixels at 120 $\mu$ m are presented in Figure 4.8.

**Figure 4.8:** The measured intensity distribution for each pixel in the C_120 filter by rastering the planetary nebula NGC7027 which is assumed to be a point source for ISO. The footprints have been normalised to 1 at the peak position. Contour levels are 2.5, 5, 10, 12.5%, 20 to 90 with step of 10%, and 98% of peak.
$\resizebox {10cm}{!}{\includegraphics*[70,245][535,670]{c120footmap.eps}}$

The measurements were compared with a theoretical model based on the telescope point spread function measured with ISOCAM. The model assumes a two mirror f/15 telescope with radii for the primary and secondary mirror of 30 and 10 cm, respectively. It includes the stray cones of the secondary's support tripod (Okumura 2000, [44]). The model footprint is calculated from the convolution of the point spread function with the pixel surface. Comparison between the predicted and the measured footprint shows good agreement. The inferred effective solid angles of the pixels are all larger by 20 - 60% than the values given in Table 9 of the `ISOPHOT Observers Manual' 1994, [21]. This can be understood by the broadening of the point source profile due to infrared light scattered by the support legs.

The effective solid angle enters the extended source calibration in the conversion from Jy/pixel to MJy/sr, see Section 5.3.

4.5.1.2 PHT-P footprints

Scanning a point source over a number of the PHT-P apertures with stepsizes much smaller than the size of the apertures has revealed that the footprints of the apertures are not simple top-hat functions as suggested in Figure 2.2, but show strong irregular variations as a function of aperture radius. The variations are illustrated in Figure 4.9 where the scans over the largest aperture in the 7.3 and 12.0 $\mu$ m filters are presented.

Figure 4.9: Left panels: Aperture profile scans at 7.3 $\mu$ m, 180 aperture on the star HR 1396. Error bars indicate the signal reproducibility in the forward and backward scans. Note that the background signal level has not been subtracted in all panels. Right panels: Aperture profile scans at 12.0 $\mu$ m, 180 aperture on the star HR 0440.

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{muellert1_4.ps}}}$

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{muellert1_5.ps}}}$

Figure 4.9 clearly shows that the energy of a uniform extended source in a given aperture is not necessarily proportional to the area of the aperture. Moreover, the flux density of an extended source with a size similar to the aperture depends on the position of the peak of its infrared brightness distribution in the aperture. E.g. in the case of the 12 $\mu$ m filter combined with the

aperture, the sensitivity at position (

) is some 5 times larger than at (

). Due to the large amount of possible filter/aperture combinations only a few cases have been investigated as detailed as presented in Figure 4.9 (Müller 2000a, [41]).

Not only the accuracy of the sky brightness measurements suffer from the irregular apertures, also the FCS calibration measurements require a separate calibration for the relation between power on the detector and aperture area for different levels of the FCS heating power. A complicating effect is that the illumination of the aperture by the FCS can be inhomogeneous (see also Section 4.5.4) as is observed for the C100 and C200 detector arrays.

Due to the irregular properties of the PHT-P apertures, the point source calibration in non-standard apertures and the extended source calibration of PHT-P have not been scientifically validated. An investigation of PHT04 aperture sequences on point and extended sources can be found in Müller 2000a,b, [41], [42].

4.5.1.3 PHT-S footprints

The size of the PHT-S aperture ( $24''{\times}24''$ ) has been designed to mask the part of the sky which is directly mapped onto the PHT-S pixel at a given wavelength. In-orbit observations have shown that the PHT-S response is very sensitive to pointing variations perpendicular to the dispersion direction which is along the spacecraft Y-direction (see Figure 4.10).

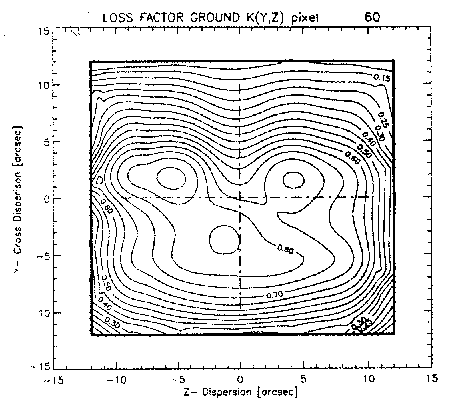
By scanning a point source over the PHT-S aperture in Y and Z-direction, and assuming axisymmetry, PHT-S footprints have been determined for each pixel of both the SS and SL arrays. The resulting profiles show that the general shape of the PHT-S footprints are sharply peaked in non-dispersion direction (spacecraft Y-direction). The profile in dispersion direction (spacecraft Z-direction) is flatter over the aperture. These in-orbit calibrations confirm the results of ground-based measurements of the beam profiles. An example of a footprint measured on ground is given in Figure 4.10.

Another feature of the PHT-S footprints is that not all peak at the centre of the aperture. For some pixels the centre of the array is on a steep flank of a footprint. As a result, the shape of the spectrum strongly depends on the exact pointing in Y-direction. For example, in case of pixel 60 (Figure 4.10) a pointing error of ${\pm}$ 3 arcsec in Y direction can cause a change in response of the order of 20%.

The PHT-S spectral response function used in the OLP is only valid for the centre position of the PHT-S aperture. Corrections for pointing offsets can be applied using the footprints of the individual pixels.

**Figure 4.10:** Two dimensional beam profile of PHT-S pixel 60 as measured in the ISOPHOT ground calibration facility. This is an example where the intensity maxima are multiple and are off the major axes. In-orbit cross-scans along the major axes were performed which show qualitatively the same behaviour: a relatively flat and symmetrical shape in the dispersion direction and a slightly off-centre and steeply falling-off profile in cross-dispersion direction.
$\resizebox {7cm}{!}{\includegraphics{spix602dbeam.eps}}$

Based on the footprints of all PHT-S pixels the correction factors for the transformation from point source flux to extended source surface brightness have been derived. A homogeneous illumination of the PHT-S aperture is assumed.

4.5.2 Point source intensity fractions

The intensity fractions, or $f_{psf}$ , of a point source passing through a given filter/aperture combination of PHT-P or filter/pixel combination of PHT-C has been calculated using a simplified model of the point spread function. This model assumes a uniformly illuminated round mirror of 30 cm radius with a f/15 focal length and a central obscuration of 10 cm radius. The sizes of the apertures and detectors as determined on ground together with the central wavelength of the filters have been used to determine $f_{psf}$ .

For C200 the fraction of light falling on the whole array is significantly different from the fraction calculated for the model described above in which the physical dimension of the detector arrays have been included. This is probably due to losses and diffraction at the inter-pixel gaps of order 100 $\mu$ m when the point spread function is centred on the C200 array and not on one of the pixels. Empirical correction factors obtained from calibration observations have been determined to correct for this effect (Laureijs 1999, [32]).

The resulting values for $f_{psf}$ are stored in a Cal-G file, see Section 14.18.

4.5.3 Chopper vignetting/offset

Although the guaranteed unvignetted field of view for the ISO instruments is 3 arcmin, PHT can have chop throws up to $\pm$ 90

for the largest aperture of 180

and $\pm$ 165

for the smallest aperture w.r.t. the CFOV. It is therefore expected that for larger chopper throws corrections should be made for possible vignetting of the chopper beams. As the chopped beam has a different ray path through the telescope-instrument system additional chopper offsets can occur which have been observed, too.

The combined effect of chopper vignetting and chopper offset can cause a relative signal difference between the on- and off- chopper beams for an otherwise flat sky. As a consequence, chopped observations of faint sources which are only a few percent brighter than the sky background can only be analyzed after correction for these effects.

Calibration observations indicate that chopper offsets for the PHT-P detectors are small: less than 1% flux difference between the chopper positions for a flat sky. For the PHT-C detectors, the offsets depend on the chopper throw and can become substantial for the largest amplitudes (as high as 6%). Note that maps obtained with PHT32 need to be corrected for this effect.

4.5.4 Inhomogeneous FCS illumination

The detectors are not homogeneously illuminated by the FCS. For the PHT-P detectors the measured flux does not scale proportionally with the aperture area, while for the PHT-C detectors the different pixels are not receiving the same in-band power. Illumination matrices or factors for correcting the inhomogeneous illumination over the 180 arcsec field of view have been determined for each filter/detector/aperture by in-flight measurements.

The FCS illumination matrix is filter dependent. As a consequence, when using an FCS measurement made e.g. in the C_90 band to calibrate a measurement made in the C_60 band, the filter dependent flat-fields have to be accounted for, see Section 4.2.7.

For the PHT-P detectors strong deviations from a linear scale have been measured when changing the FCS aperture while maintaining the same FCS heating power. The calibration of the FCS against astronomical standards has been performed only with a few selected apertures, see Section 5.4.

Studies with a limited set of calibration data have indicated that the deviations from a linear scale can be as high as 20% for detectors P2 and P3. For P1 the effect can even be stronger, upto a factor 2. This means that a systematic error in the photometric calibration is made when using apertures for the FCS measurements that are different from the standard ones listed in Section 5.4.

The corrections using illumination matrices for C100 and C200 are included in the SPD processing, see Section 14.14 for a description of the related Cal-G file.