Subsections

• 5.9.1 The beam profile
• 5.9.2 Asymmetry
• 5.9.3 Flux correction for extended sources
• 5.9.4 Extended source flux per unit area
• 5.9.5 Effect of the ISO PSF at large distances: check of the straylight around Jupiter

5.9 Instrumental Field of View: The Beam Profile

Figure 5.16: Offset positions of the Mars beam profile observations.

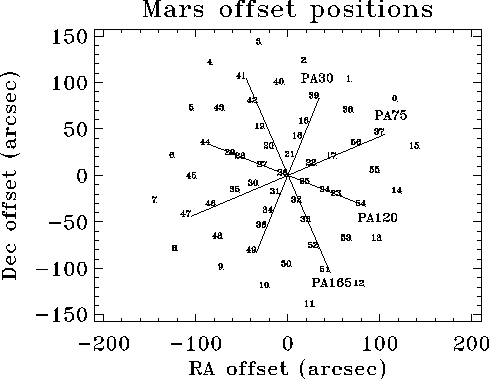
The beam profile has been derived from a series of standard bias, grating scan observations of Mars. One observation was made on-axis and the others were distributed around the field as shown in Figure 5.16. The flux at three wavelengths in each detector, at each of the raster positions, are used to describe the radial sensitivity of the instrument and a parameterisation defines the beam profile. In addition subsets of the data along the four radial alignments, which are labelled PA30, PA75, PA120 and PA165 on Figure 5.16, have been analysed to investigate possible asymmetries in the beam profile.

Before discussing the beam profile it is important to appreciate the properties of the optical path leading to the LWS detectors as these have a profound impact on the beam profile. The optical train of the LWS consist of the contour field mirror that allows a beam of 120 to fall on the complex mirror M2, which is inclined at 22 to the incoming beam. M2 diverts the beam by 44 back through a semi-cylindrical cut-out in the contour field mirror and then presents an elliptical beam of 105 97 (nominal FWHM) to the collimator, the LWS entrance pupil, the re-imaging mirror and detectors. Immediately in front of each detector is a rectangular aperture with rounded ends, which when projected onto the sky is approximately elliptical with dimensions of 104 157 at SW1 and 138 131 at LW5 in the directions along and across dispersion respectively. The long and short axes of M2 projected onto the sky are PA30 and PA120 (Y and Z axes) respectively.

As the detector apertures are nominally larger than the incoming beam from M2 it is, in fact, M2 that defines the aperture of the detectors, and the character of the optics determines the instrumental profile. Perversely, the substrate that supports M2 is also reflective, particularly at longer wavelengths, and is now believed to be responsible for the fringing that is seen in off-axis targets. A second consequence of this is that the instrumental profile will have weak wings out to 120 diameter (the size of the contour field mirror).

The other feature of LWS grating spectra of objects observed off-axis is the poor stitching between adjacent detectors, which is often referred to as fracturing. The problem is apparently worse for objects in the part of the field that passes close to the cut-out in the contour field mirror. The origin of this problem is unknown but it introduces a complex, wavelength-dependent asymmetry into the instrumental profile. These problems are described in more detail in Sections 6.2 and 6.3.

5.9.1 The beam profile

The observed beam profile is the result of the convolution of the telescope PSF and the instrumental profile of each detector. Ideally the telescope PSF would be an Airy profile but the central obscuration and secondary supports, and any optical imperfections will conspire to redistribute power from the core of the profile to the Airy rings. Although a point source is being used to probe the structure of the beam, the width of the PSF, which is essentially an Airy profile, increases from 25 to 100 (FWHM) between 46m and 178m, and at the longer wavelengths becomes comparable with the size of the beam. Due the problems of fracturing and fringing the true shape of the instrumental profile is largely unknown.

Figure 5.17: The beam profiles for the central wavelength of each detector. The observed relative flux at each offset position is plotted against radius, with the sign taken from the RA offset in Figure 5.16. The line on each plot shows the calculated radial profile.

To determine the effective beam size the observed fluxes at three wavelengths in each detector have been compared with those derived from a convolution of the telescope PSF with apertures of various sizes. The latest model of the telescope PSF includes the effects of the central obscuration and its supporting structure, and indicate that the power in the Airy rings is increased and that the wings of the profile contain 2-D structure. The asymmetry introduced into the profile is due to the three-legged secondary support. The aperture has been assumed to be circular with a rectangular profile.

It has previously been recognised that the effective apertures are significantly smaller that the nominal value of 100 , based on the size of the beam from M2. The best value for most of the detectors lies close to 80 , and for LW3, LW4 and LW5 is somewhat smaller than this. At the longest wavelengths the width of the telescope PSF is larger than the aperture itself which makes these determinations more difficult. An uncertainty of one arcsec in the radius corresponds to about 5% in the effective area of the aperture.

Also, although a simple circular aperture has been adopted, more complex shapes can provide a better description of the asymmetries, under some circumstances. However, the range of possible shapes and number of free parameters makes this approach untenable.

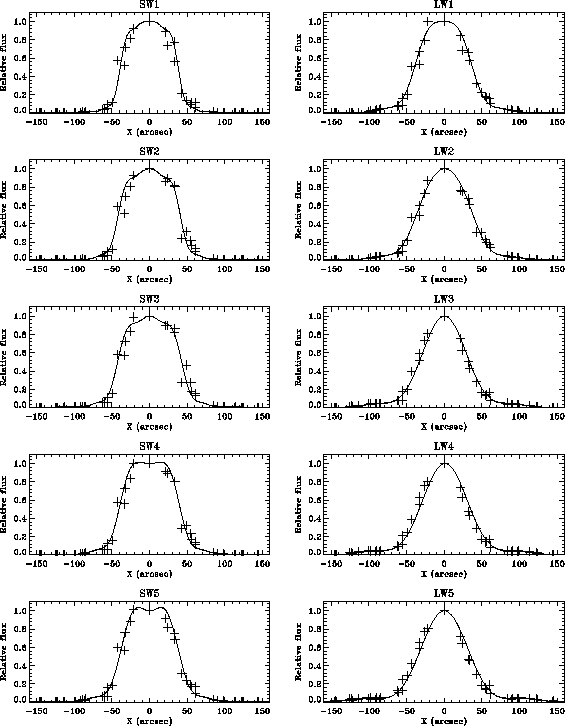
The relative flux at each of the observed offset positions (see Figure 5.16) is shown for each detector in Figure 5.17 with the convolution of the telescope PSF and the best fit composite aperture superimposed. At shorter wavelengths the telescope PSF is narrow enough to probe the structure of the rectangular (top hat) instrumental profile and some indication of its shape can be seen. As the telescope PSF broadens towards longer wavelengths the details of the instrumental profile become washed out and the observed profile becomes more Gaussian.

The resulting estimates for the effective beam size for each detector are given in arcsec in Table 5.9.

Table 5.9: Effective aperture of the detectors.

Detector	Effective	Detector	Effective
	radius [ ]		radius [ ]
SW1	39.4	LW1	38.6
SW2	42.3	LW2	38.9
SW3	43.5	LW3	35.5
SW4	40.9	LW4	34.7
SW5	39.5	LW5	33.2

The effective solid angle of the detectors is required to determine the point/extended source flux correction, for the conversion of observed flux to flux per steradian for extended sources and for the calibration of sources observed in parallel and serendipity mode (see Table 5.10).

5.9.2 Asymmetry

It is already clear from Figure 5.17 there is some asymmetry in the beam profile, with groups of points lying systematically off the lines. The question of symmetry is not straightforward, and a simple analysis of the relative mean fluxes for the four radial alignments begins to show this.

Each of the radial alignments is a subset of the data which define the global mean profile. The four alignments are separated by approximately 45 to create two orthogonal pairs, with the PA30 set aligned along the Y axis, and the PA120 set aligned along the Z axis of M2. A Gaussian profile constrained to the optical axis was fitted to each set with the on-axis point and those with excluded. Although each alignment contains nine points, only six points are used in the PA30 and PA120 solutions and only four points in the PA75 and PA165 solutions.

Figure 5.18: FWHM vs. detector for the four alignments.

Of the parameters derived from these solutions the FWHM is probably the most reliable, and this is shown in Figure 5.18 for the different detectors. Although there is considerable scatter the behaviour is fairly consistent. Each alignment shows an increase in FWHM through the SW detectors and then a subsequent decline, which reflects the behaviour of a Gaussian fit to all the data, and the run of effective aperture sizes in the table above. In more detail it can be seen that the alignments fall naturally into two pairs with very similar behaviour. PA75 and PA120 show much more variation than PA30 and PA165, and peak at SW3 as opposed to SW5. In particular PA75 and PA120 run through the fractured region; see the spectra in Figure 6.3 of raster positions 27 and 30 in Figure 5.16.

5.9.3 Flux correction for extended sources

The LWS flux scale is based on a point source calibration, although beyond the diffraction limit at about 110 m a substantial fraction of the flux from an on-axis point source is diffracted out of the aperture. In fact there are significant diffraction losses for all LWS detectors but provided the calibration is applied to point sources observed on-axis these losses are irrelevant because they are cancelled out in the calibration process. However, for extended sources the diffraction losses do not occur and so a correction has to be applied to correctly place the derived fluxes on the point source calibration scale. The correction factor to apply to the fluxes in case of extended sources has been calculated at three wavelengths per detector. These factors are given as in Table 5.10.

5.9.4 Extended source flux per unit area

To convert the observed flux of an extended source to flux per steradian requires both the extended source correction factor (, see above) and the effective aperture in steradian explicitly.

Table 5.10: Table of extended source correction () and effective solid angle of the beam () for the different LWS detectors, at three different wavelengths per detector. The effective aperture radius in arcsec () is also given at the same wavelengths.

Detector	m]		r [ ]	[sr]
	43.0	0.8721	39.3	0.1140
SW1	46.2220	0.8704	39.4	0.1146
	50.0	0.8691	39.4	0.1146
	50.0	0.8705	42.6	0.1340
SW2	56.2033	0.8677	42.3	0.1321
	60.0	0.8563	42.1	0.1308
	60.0	0.8634	43.5	0.1397
SW3	66.1173	0.8421	43.7	0.1410
	70.0	0.8127	43.4	0.1390
	70.0	0.7845	41.2	0.1253
SW4	75.6989	0.7334	40.7	0.1223
	80.0	0.7118	40.9	0.1235
	80.0	0.6904	38.4	0.1088
SW5	84.7977	0.6878	39.7	0.1163
	90.0	0.6803	40.3	0.1199
	90.0	0.6753	38.3	0.1083
LW1	102.425	0.6758	38.8	0.1111
	108.0	0.6757	38.6	0.1100
	108.0	0.6761	39.6	0.1157
LW2	122.218	0.6734	39.1	0.1128
	130.0	0.6557	38.1	0.1071
	130.0	0.6445	36.5	0.0983
LW3	141.809	0.6035	35.6	0.0935
	150.0	0.5623	34.3	0.0868
	150.0	0.5727	35.3	0.0920
LW4	160.554	0.5411	35.0	0.0904
	170.0	0.4855	33.9	0.0848
	170.0	0.5002	34.3	0.0868
LW5	177.971	0.4596	33.6	0.0833
	195.0	0.3749	31.6	0.0737

The corrected extended source flux for an observed flux given in Jy is MJy/sr, where is the extended source correction and is the effective solid angle of the beam in sr. These values are now given at three different wavelengths per detector (from Version 2.1 of this volume of the ISO Handbook on). As visible on Figure 5.19, for most detectors the resulting correction factor presents a gradient with wavelength. This has the positive consequence that with this correction there is a better agreement between the corrected fluxes of extended sources in the overlap regions between detectors.

Figure 5.19: Correction factor for extended sources ( ) versus wavelength. The correction factor is given at three different wavelengths per detector. Detectors are given alternately in red and blue; red, SW1, SW3, SW5, LW2, LW4, and blue, SW2, SW4, LW1, LW3 and LW5.

An LIA routine has been provided that applies this correction to averaged, de-fringed LSAN files called EXTENDED_FLUX. However, these corrections are derived under the assumption of a smooth and very extended flux distribution. In the real world, structured or embedded sources could produce significant discrepancies from the ideal situation, and, with it, differences in flux.

Figure 5.20: Comparison of LWS and IRAS 100 m fluxes in the Trumpler 14 (red diamonds) and 16 (black diamonds), and Galactic Centre (blue squares) fields.

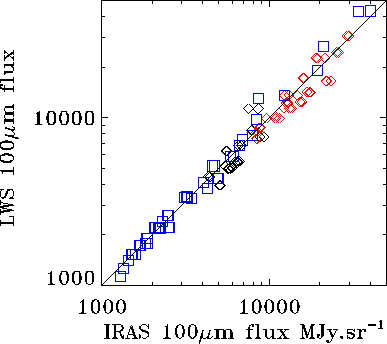
LWS observations have been made at a number of positions in the Trumpler 14 and 16, and Galactic Centre fields and these have been compared with the IRAS 100 m fluxes at the same positions. Both fields contain a large area of extended emission, which although relatively smooth, does change by a factor of 40 over all. Figure 5.20 shows the comparison of the converted LWS and IRAS 100 m fluxes using the current LWS calibration. These measurements give a mean ratio, LWS/IRAS 1.00.1. Ideally for this comparison the extended flux should be distributed as evenly as possible, and part of the uncertainty is probably due to unresolved structure within the beam.

For fields containing multiple sources the observed flux will depend critically on the precise positions of the sources relative to the optical axis. To recover or model the observed flux will require positional information on the sources and a deconvolution with the telescope PSF and instrumental profile. Indeed, for single point sources observed off-axis a similar procedure will be required to recover the correct flux.

5.9.5 Effect of the ISO PSF at large distances: check of the straylight around Jupiter

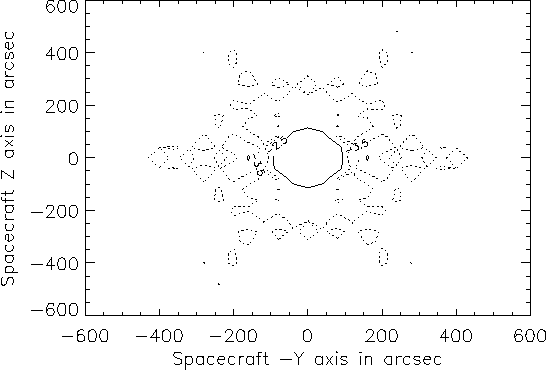
A complete study of the beam profile of the LWS has been performed only for distances within 150" of the central source. Rasters of larger extent would have been too time-consuming. There were, however, spot checks of the flux entering the instrument at even larger distances from a very strong source: The off-position spectra for Ganymede and Callisto. They provide us with the fluxes from Jupiter, when the aperture of the LWS was pointed at distances of 5' and 9' from this planet. The results are shown in Table 5.11 and compared to the fluxes expected from a model of the PSF by Okumura 2000, [30]; see Figure 5.21.

Table 5.11: Flux at a certain distance of Jupiter normalised by the flux of Jupiter: Comparison of LWS observations of Jupiter straylight with a model of the ISO PSF by Okumura 2000, [30].

		SW2	model	LW2	model
Distance	Angle to S/C Z
[arcsec]	[]
282	38	860	77	1100	406
291	325	440	94	890	125
530	113	84	14	300	66
532	20	38	0.1	100	25
535	2	27	5.5	52	8
537	148	73	13	350	26
545	344	53	2.8	190	52

The significance of the correlation between the measured flux and the model PSF is 2.4  for detector SW2 at 56 m and 2.6  for detector LW2 at 122 m. The correlation between flux and distance or angle alone is much weaker, hence the model PSF reflects correctly the observed flux pattern up to a distance of 9 from the source. On the other hand the measured fluxes are systematically higher than what is expected from the optical model, which could be due either to the fact that Jupiter is not a point source or to the existence of significant wings in the beam profile.

Figure 5.21: A model of the point spread function as sampled with the LWS. The contours show the drop in intensity by factors 10 (continuous line) and 10 (dotted line) compared to the on-source value.