next up previous contents index
Next: 4.2 Dark Current Up: 4. Calibration and Performance Previous: 4. Calibration and Performance

Subsections


4.1 Responsivity


4.1.1 Absolute flux calibration

The absolute flux calibration of the ISOCAM instrument is based on observations of standard stars, which are believed to be the most reliable calibration sources in the 2-18 $\mu$m ISOCAM wavelength range. Before and during the ISO operations, Spectral Energy Distributions (SEDs) were provided by Martin Cohen (Cohen et al. 1992, [18]; 1995, [19] and 1996, [20]) and through an extensive pre-launch `Ground Based Preparatory Programme' (GBPP), led by Prof. Harm Habing (Jourdain de Muizon & Habing 1992, [39]; van der Bliek et al. 1992, [61]; Hammersley et al. 1998, [36] and Hammersley & Jourdain de Muizon 2001, [37]). Later, additional SEDs were provided by Dr. Leen Decin who, through an iterative process using SWS data, produced a set of MARCS model synthetic spectra (Decin 2001, [25]; Decin et al. 2003a, [26]). The absolute flux calibration of the various models delivered is estimated to be better than 3%. A discussion on a comparison of the different provided models can be found in Decin 2001, [25]. The determination of the CVF Spectral Response Function (SRF) is discussed in Section 4.8. The fixed filters calibration relied mainly on the model spectra from the GBPP. In the GBPP, Kurucz models were fitted to the visible and near-infrared data to provide flux densities at longer wavelengths. Mostly, early- or intermediate-type stars were selected (A, F, G) and not late-type giants which can show strong molecular absorption band features which are not well addressed in the Kurucz models (Blommaert 1998, [10]). A wide range of stars with different flux densities was used (ranging from 10 mJy up to 10 Jy). In order to be able to revisit the stars regularly, they were selected from a region of sky with an almost 100% visibility to ISO (R.A. $\approx 16$ hrs, DEC $\approx +55$). Because of the high sensitivity of ISOCAM and the resulting higher risk for saturation, generally weaker and thus somewhat less well studied standard stars were observed. For cross-calibration with other (ISO) instruments some of the brighter calibration stars were observed in the few filters which did not saturate the camera for such bright sources. The flux calibration observations were done in staring mode with the source at the centre of the array. Data analysis of the standard star measurements was performed within the CIA package and followed a standard procedure, including: deglitching (method=`temp'), averaging the frames on the stabilised part of the measurement, flat-field correction and background subtraction. A more detailed description of the observations and the selection of the standard stars used for the calibration of the fixed filters can be found in Blommaert 1998, [10] and Blommaert et al. 2000, [11]; 2001b, [13]. The conversion from measured signal in ADU/G/s to flux density in Jy is conveyed in the so-called SENSITIV parameter which can be found in the calibration file CCG*SPEC (see Section 6.1.6). 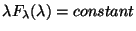The conversion factor is given for the reference wavelength of each filter, assuming a $\lambda F_{\lambda}(\lambda) = constant$ spectrum. Formally the reference wavelengths are arbitrary and they have been chosen so that they clearly identify each filter and are easy to remember. Some reference wavelengths (for the filters: SW1, SW2, LW6, LW8 and LW10) are chosen for comparison with the ISOPHOT filters. The LW10 filter gives also a direct comparison with the 12$\mu$m IRAS filter. For further details see Moneti et al. 1997, [42]. Tables 4.1 and 4.2 give the the reference wavelengths and the values of the SENSITIV parameter for the LW and SW filters, respectively. The observed spread in the SENSITIV parameter, also indicated in these tables, is caused by two factors. One is the uncertainty in the extrapolation of the near-infrared fluxes on the basis of the Kurucz models. The second is the difference in stabilisation of the signal of the various observed calibration stars. Although special care was taken to ensure that the signal had stabilised, uncertainties of the order of 5% remain.


Table 4.1: LW SENSITIV values.
Filter 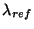$\lambda_{ref}$ Mean rms
  [$\mu$m] [ADU/G/s/mJy] [%]
LW1 4.5 0.77 4.1
LW2 6.7 2.32 3.3
LW3 14.3 1.96 4.8
LW4 6.0 0.78 7.5
LW5 6.8 0.35 7.5
LW6 7.7 1.03 6.4
LW7 9.6 1.33 6.7
LW8 11.3 0.78 5.4
LW9 14.9 0.65 2.8
LW10 12.0 4.23 3.9


Table 4.2: SW SENSITIV values.
Filter 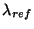$\lambda_{ref}$ Mean rms
  [$\mu$m] [Adu/G/s/mJy] [%]
SW1 3.6 0.41 4.6
SW2 3.3 0.12 4.9
SW3 4.5 0.26 3.4
SW4 2.8 0.30 2.9
SW5 4.0 0.77 4.8
SW6 3.7 0.19 6.0
SW7 3.0 0.16 4.5
SW8 4.05 0.038 7.2
SW9 3.9 0.074 5.8
SW10 4.6 0.092 2.5
SW11 4.26 0.058 5.5


4.1.2 Trends in the responsivity

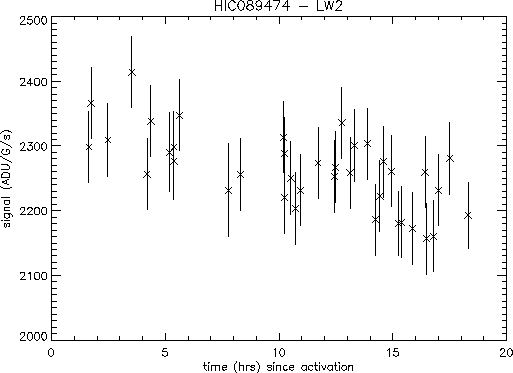
The responsivity was monitored through the mission by regularly observing the star HIC 89474 (= HR 6847) (Blommaert 1998, [10]). Filters used were LW2, LW10 and SW3. The same source was also observed throughout the spacecraft orbit, to check for possible variations as a function of the orbit phase. Figure 4.1 shows all the LW2 photometric measurements of HIC 89474 as a function of time since instrument activation, following passage of the satellite through the Van Allen belts. There is a trend of decreasing responsivity with time since activation. The difference between the response at the start of the revolution and at the end is about 6%. This value is included in the CCGLWLOSS calibration file (see Section 6.1). 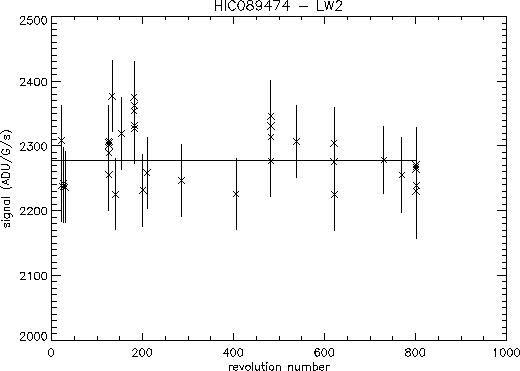Figure 4.2 shows the LW2 photometry, corrected for the in-orbit trend in responsivity, and running up to revolution 801. The difference between the maximum and minimum level is less than 10% and the overall rms is 2%. There is no trend in the responsivity as a function of time through the mission, the only trend being the intra-revolution drift already described. The same conclusion holds for the LW10 measurements (and concerning the in-orbit trend, also for LW1 which was observed repeatedly on revolution 349) so that we believe that this is the general behaviour of the LW detector. SW also shows only a small variation throughout the mission (rms = 2%) and no significant trend is found.

Figure 4.1: Photometry in the LW2 filter of HIC 89474 as a function of time since activation. There is a trend of decreasing responsivity along the orbit.
\resizebox {12cm}{!}{\includegraphics{lw2_tsa_trend.ps}}

Figure 4.2: Photometry in the LW2 filter of HIC 89474 throughout the mission as a function of revolution number. The photometry is corrected for the decrease of responsivity which occurred throughout the orbit. No significant change in responsivity through the mission is found.
\resizebox {12cm}{!}{\includegraphics{lw2_mission.ps}}

The response of the detectors was also monitored throughout the mission by measuring the ICD during each de-activation sequence at the end of a revolution. The trend analysis shows that the SW responsivity was very stable and decreased by at most 0.5% over the mission (Gallais & Boulade 1998, [35]; Boulade & Gallais 2000, [14]). The mean level of the LW `flat-field' measurements showed a slow decrease of about 0.8% per 100 revolutions. With these measurements it is difficult to distinguish the trend of the responsivity of the detector from any trend in the ICD emissivity. Considering the fact that the measurements of standard stars did not show such a decrease it seems likely that this effect comes from a change in characteristics of the LW ICD itself.


4.1.3 Responsivity and observing parameters

Observations were made to test whether any relationship could be found between the responsivity and different configurations of the camera. No, or only marginal, differences were found between different pfov's or different on-chip integration times for both detectors (Blommaert 1998, [10]; Blommaert et al. 2000, [11]).
next up previous contents index
Next: 4.2 Dark Current Up: 4. Calibration and Performance Previous: 4. Calibration and Performance
ISO Handbook Volume II (CAM), Version 2.0, SAI/1999-057/Dc