Next: 4.7 Spacecraft Pointing Jitter Up: 4. Calibration and Performance Previous: 4.5 Flat-Fields

4.6 Point Spread Function (PSF)

4.6.1 Observed PSFs

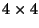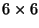Point source observations were performed with a $4\times4$ micro-scan raster with a step size of 3 $^{\prime \prime }$ for 12 $^{\prime \prime }$ pfov, and with a $6\times6$ micro-scan raster with step size of 2 $^{\prime \prime }$ for the other pfov's, in order to obtain a good spatial sampling of the PSFs. However, due to the undersampling of the PSF inherent to some CAM configurations, this did not allow a fine enough sampling of the PSF for every optical configuration. Therefore, users should be aware of this if attempting to use a library PSF for deconvolution purposes. The micro-scan raster used for the PSF measurements also yields information about photometric variations as a function of the position of the point source within a single generic pixel. The raster spans several pixels, and the point source assumes a range of positions with respect to the various pixels centres. If pixels are assumed to be identical with respect to the variation of response across their surfaces, then the overall raster can be seen as building-up a set of PSFs with families specific to particular relative positions of point source and pixel centre (`sub-pixel positions'). Except for the 12 $^{\prime \prime }$ pfov, one raster contains 9 sets of 4 raster points with equivalent sub-pixel positions, within a localised group of pixels. One PSF is constructed by averaging these four point source images. This led, within the detector region covered by each raster, to a set of 9 PSFs expressing the appearance of a point source for each of the 9 particular sub-pixel positions. Therefore, the PSF library contains one set of 9 PSFs for each detector zone rastered for each configuration calibrated. Figures 4.14 and 4.15 show examples of the micro-scans performed for 3 $^{\prime \prime }$ and 6 $^{\prime \prime }$ pfov PSF measurements. All the rasters for a given optical configuration were done within one observation time block, pointing on the same star.

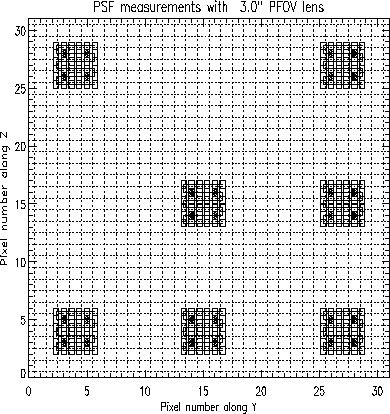
**Figure 4.14:** *PSF measurements on different regions of the detector for the 3 $^{\prime \prime }$ pfov*
$\resizebox {9.5cm}{9.5cm}{\includegraphics{rstrs3.ps}}$

**Figure 4.15:** *PSF measurements on different regions of the detector for the 6 $^{\prime \prime }$ pfov*
$\resizebox {9.5cm}{9.5cm}{\includegraphics{rstrs6.ps}}$

All the PSFs of a given configuration are normalised by the flux of the central PSF. This global normalisation factor describes a photometric correction that would need to be applied to point sources as a function of distance from the array centre and/or as a function of source barycentre on the central pixel of the point source. For each configuration, only one PSF is normalised to 1. The normalisation factor is the integrated flux of the reference PSF, excluding the edge pixels. A detailed description of the observations and analysis made can be found in the ISOCAM PSF Report (Okumura 1998, [44]).

4.6.2 Model PSFs

In the optical PSF model computation, the pupil image is created in Fourier space. The pixel size 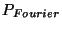$P_{Fourier}$ in this space is given by:

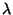$\begin{displaymath}P_{Fourier} = \frac{\lambda}{S \cdot P_{rad}}\end{displaymath}$

where $\lambda$ is the reference wavelength of the filter bandpass,

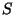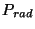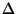is the square size of the applied image dimensions expressed by the number of pixels and $P_{rad}$ is the pixel size of the image in the direct space in radians. The diameter $\Delta$ of the circular aperture in Fourier space, in pixel units, is then given by dividing the telescope diameter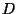

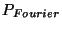by the pixel size $P_{Fourier}$ :

$\begin{displaymath}\Delta=\frac{D}{P_{Fourier}}=\frac{D}{\lambda}S \cdot P_{rad}\end{displaymath}$

If 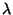$\lambda$ is expressed in $\mu$ m, its radius is given by:

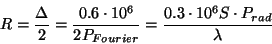$\begin{displaymath} R=\frac{\Delta}{2}=\frac{0.6\cdot 10^{6}}{2~P_{Fourier}}= \frac{0.3\cdot 10^{6}~S \cdot P_{rad}}{\lambda} \end{displaymath}$

(4.2)

In order to execute a correctly sampled computation both in Fourier space and in direct space, it is necessary to create a finer sampling and a larger image size than the real image coming from the ISOCAM detectors. If, in addition, one wants to add the detector pixel convolution effect on the optical PSF model, then the sampling in direct space should be better than at least half of the pixel size. Once the image size is chosen, the central obscuration and the tripod structure (supporting the secondary mirror of the telescope) are added to the main aperture model. The Fourier transform of the aperture then gives the optical PSF which will be convolved by the detector pixel size and resized to the real dimension of the detector array. For more accurate models, one should integrate over the bandpass profile of each filter multiplied by the spectral energy distribution of the source. However, the theoretical and monochromatic PSF constructed here, can be well compared with the observed PSF as long as the bandpass is not too wide. Thus, the model applied here neglects the impact of the filter bandpass on the shape of the final PSF. In Figures 4.16, Figure 4.17 and Figure 4.18 the theoretical and the measured PSFs are compared. Details are given in the ISOCAM PSF Report (Okumura 1998, [44]). A comparison of the FWHM of the model (Figure 4.17) and measured PSF (Figure 4.18) to the Airy disk diameter of the ISO telescope demonstrates that a good reproduction of the PSF is obtained for all ISOCAM filters except for LW10 and LW1. The deviation observed in LW10 could be an effect of the very wide bandpass while the anomaly in LW1 is not yet understood.

**Figure 4.16:** *Comparison of the measured and the modelled PSF for the LW9 filter and the 3 $^{\prime \prime }$ pfov*
$\resizebox {13cm}{10cm}{\includegraphics{big3lw9.ps}}$

**Figure 4.17:** *FWHMs of the modelled PSFs. The dashed line is the Airy disk diameter (Section 2.1).*
$\resizebox {12cm}{!}{\includegraphics{modlfwhm.ps}}$

**Figure 4.18:** *FWHMs of the measured PSFs. The dashed line is the Airy disk diameter (Section 2.1). The horizontal bars indicate the bandwidth of each filter.*
$\resizebox {12cm}{!}{\includegraphics{psf_fwhm.ps}}$

Next: 4.7 Spacecraft Pointing Jitter Up: 4. Calibration and Performance Previous: 4.5 Flat-Fields

ISO Handbook Volume II (CAM), Version 2.0, SAI/1999-057/Dc