Next: 6.10 Detector Non-linearity: the Up: 6. Caveats and Unexpected Previous: 6.8 `Detector Warm-up Features'

Subsections

6.9 Transients and Memory Effects

6.9.1 Description

All LWS detectors presented some level of memory effects, also called transient effects, due to the slow response times (typically tens of seconds) to changes in illumination (Church et al. 1992, [7]). These non-linear effects were more severe for the Ge:Be detector (SW1) and some of the stressed Ge:Ga detectors (LW2-LW5). The response of the detectors depended not only on illumination level, but also on the illumination history. The transient effects could be enhanced by intrinsic spectral characteristics of the observed astronomical source, but also by strong glitches or fringes. A good illustration of the response times of the detectors is given by the time series of L02 fixed grating observations, where each detector remains at one wavelength and thus sees the same flux for a long time. Figure 6.7 (from Müller 2001, [29]) shows typical examples of transients in such fixed grating observations. In this mode of operations, the transients are easy to correct for, but it is much more difficult for a normal scanning mode, where the illumination experienced by each detector changed every half-second and the detectors never had time to stabilise.

The best way to correct the transient effects in spectra would have been to handle a complete physical model of each detector as well as a complete knowledge of the detector illumination in all observing conditions (see Coulais & Fouks 2001, [10]). However, there was no such model available for LWS detectors.

Figure 6.7: Transient examples, taken from L02 fixed grating observations of Uranus and Neptune. Only the first 300s are shown. One can distinguish between short term transients (first 50 to 100s) and the long term responsivity drifts, which are not even stabilised after 1500s (mainly LW4 and LW5). A reference flux value (triangle) was calculated for the integration time between 100 and 150s.

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{LW1_uranus.ps}}}$

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{LW2_neptune.ps}}}$

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{LW3_uranus.ps}}}$

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{LW4_neptune.ps}}}$

$\rotatebox {90}{\resizebox{!}{7.5cm}{\includegraphics{LW5_neptune.ps}}}$

Some attempts to derive a physical model of Ge:Ga photo-conductors were done in the PHT and LWS teams before ISO launch, which were not conclusive. The use of an empirical solution has been proposed, based on the standard Fouks-Schubert model (see Fouks & Schubert 1995, [17] and references therein) derived for Si:Ga detectors, and used with success for CAM and PHT-S detectors (Coulais & Fouks 2001, [10]; Coulais et al. 2001, [11]) and for some SWS detectors (Kester 2001, [22]). The detailed report of the transient study in LWS is given in Caux 2001, [5].

In order to implement this solution the formalism of the usual Fouks-Schubert model (Fouks & Schubert 1995, [17]), has first been adapted to the specific LWS case. The original Fouks-Schubert model is written for semi-stationary fluxes. For photometric instruments, as CAM and PHT, this assumption is valid. This is not really the case for the LWS spectrometer, for which the flux varies almost continuously. However, generally the flux change from one step to the other is small and one can consider the semi-stationary state valid, assuming each step of the spectrometer to be a new constant flux level. The original Fouks-Schubert formula can then be rewritten into a more suitable form for LWS as:

$\begin{displaymath} J_n(t) = \beta J_n^{\infty} + {{(1-\beta)(J _n^{ini} - \bet... ...ty} + (J _n^{\infty} - J _n^{ini})e^{-(t - t_n) \over \tau}}} \end{displaymath}$

(6.1)

Where $J_{\rm n}(t)$ is the observed signal at the instant , $J_{\rm n}^{\infty}$ is the expected signal if no transient effects were present, $J _{\rm n}^{{\rm ini}}$ is the observed flux just after the change at the time $t_{\rm n}$ and ${\rm\tau}$ is a time `constant' which depends on the detector (we will see later that in the LWS case, ${\rm\tau}$ is not constant). We also have the continuity equation:

$\begin{displaymath} J _n^{ini} = J_{n-1}^{final} + \beta( J _n^{\infty}-J _{n-1}^{\infty}) \end{displaymath}$

(6.2)

We have tried different forms of ${\rm\tau}$ and the best results, in terms of quadratic difference between forward and backward scans, were obtained with:

$\begin{displaymath} \tau = {E \over abs(J_n - J_{n-1} )^\alpha} \end{displaymath}$

(6.3)

where , ${\rm\alpha}$ and ${\rm\beta}$ are free parameters which are intrinsic for each detector. One can note that the main difference with the original Fouks-Schubert relation is the dependence of ${\rm\tau}$ with the signal gradient and not with the signal value. The second order equation implies two solutions for the transient corrected intensity, among which we always chose the one closest to the non-corrected value as for most observations we do not expect a very strong correction.

In order to fully calibrate the transient-corrected spectra, we have derived a transient-corrected RSRF, derived as the original RSRF (Section 5.2) but based on transient-corrected observations of Uranus (see Caux 2001, [5] for more details). The differences between the transient-corrected RSRF and the original RSRF are of the order of $\pm$ 2%.

6.9.2 The correction procedure

A dedicated LIA routine has been written to allow the user to correct LWS spectra for transient effects in the case of grating observations. It is not yet implemented in the current LIA (Version 10.1) but will be in one of the next LIA releases. This routine uses the SPD products as the correction should be applied on the time series. It requires to average previously the scans (forward and backward scans separately) to ensure a good signal-to-noise level of the data to be corrected. We have checked that generally the differences seen on scans performed in the same direction are only due to noise. Sometimes, the first forward and backward scans are affected by long term transient effects (due to a prior observation of a very bright source for example), and require to be entirely zapped. It also requires a previous very careful deglitching of the data as the presence of remaining glitches can seriously hampered the correction process.

The best ${\rm\alpha}$ , ${\rm\beta}$ and parameters are computed for each observation, using the criterion that the signal recorded on forward and backward scans should be equal. The observed difference is hence supposed to be the signature of the transient effects which are different in the two scanning directions, due to the asymmetrical spectral shape of the bandpass filters located in front of the detectors or to a gradient in the spectrum.

The procedure then applies the correction simultaneously to the forward and backward averaged scans, and produces two transient-corrected spectra, one forward and one backward, which can be compared to judge how well the correction performed, and which have to be further averaged together to produce the final transient-corrected spectrum.

The LIA routine that finds the best Fouks-Schubert parameters has been tested on a wide set of different observations and was found to be stable.

**Figure 6.8:** *Variation, with the revolution number, of ${\rm \alpha}$ , ${\rm \beta}$ , and gain (in terms of quadratic difference between forward and backward scans) for Uranus observations (detector LW2).*
$\resizebox {10cm}{!}{\includegraphics{CauxE_1.eps}}$

We have used all available Uranus observations to check if the three tunable parameters vary for a given source. We have found all parameters rather constant for all observations taken with the same detector bias and the same oversampling factor, as is illustrated in Figure 6.8. The variation with bias and sampling factor is expected because the intrinsic properties of the detectors vary with the applied bias and because the parameter ${\rm\tau}$ is proportional to the signal gradient, which varies with the oversampling factor for the same input flux. As an illustration of the parameter values, the mean Uranus values for ${\rm\alpha}$ and ${\rm\beta}$ are listed in Table 6.2. They are used as starting values in the transient correction procedure but are expected to vary with the object because they depend on the spectrum gradient. (

is coupled to ${\alpha}$ and the starting value is set to 1.0)

**Table 6.2:** *Mean transient correction parameter values for Uranus, used as starting values in the correction procedure.*
Detector	SW1	SW2	SW3	SW4	SW5	LW1	LW2	LW3	LW4	LW5
${\rm\alpha}$	0.6679	0.5161	0.7788	0.7707	0.7000	0.5224	0.5382	0.4251	0.4412	0.5346
${\rm\beta}$	0.82	0.8971	0.9233	0.9033	0.9367	0.94	0.774	0.74	0.7942	0.9491

The data improvement (in terms of quadratic difference between forward and backward scans) is important for detectors presenting large memory effects (SW1, LW2 and LW3), and is smaller for the others, particularly for non-stressed Ge:Ga detectors. This improvement depends as well on the type of source observed: extended sources with large fringing are subject to a much larger improvement than point sources.

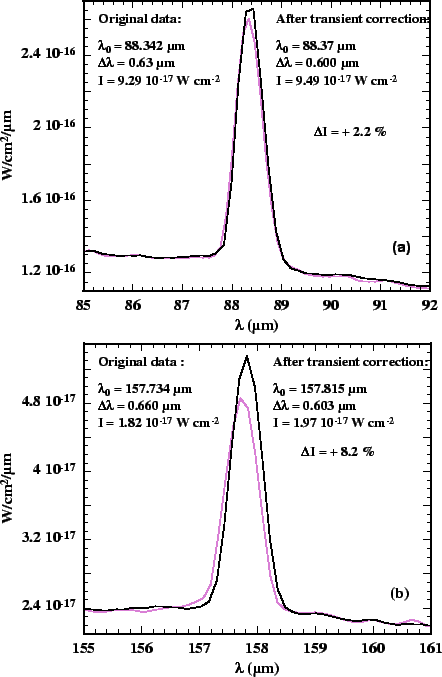
The validity of the correction has been tested on different types of astronomical sources. Figure 6.9 shows the effect of the correction on an extended source (galactic line of sight). One can note a small improvement at small scale, the remaining effects at large scale are supposed to be due to the imperfect defringing. One can also note the difference in the absolute level of the flux, which has an incidence on the stitching of the detectors.

**Figure 6.9:** *Result of the transient correction obtained for an extended source (detector LW2). Grey line: original data - black line: transient effect corrected data.*
$\resizebox {12cm}{!}{\includegraphics{CauxE_5.eps}}$

**Figure 6.10:** *Result of the transient correction obtained for a non-extended source. Grey line: original data - black line: transient effect corrected data. (a) detector LW1; (b) detector LW4.*
$\resizebox {10cm}{!}{\includegraphics{CauxE_6.eps}}$

Figure 6.10 shows the improvement obtained on strong lines for a non-extended source (a compact HII region) relative to the LWS beam. For a detector having small transient effects (LW1; Figure 6.10a), the difference on the computed line fluxes is small (a few $\%$ ) while for a detector presenting larger transient effects (LW4; Figure 6.10b), it can be of the order of $10\%$ . One can also note the more symmetrical shape of the lines after the correction, as well as a line width closer to the standard value. Finally, it can be noted that the wavelength calibration for transient effect corrected data is slightly different than the original one.

Fabry-Pérot observations with LWS were always performed (for routine observations) by scanning the spectrum in only one direction. This prevents the use of the forward and backward scan differences to derive the correction parameters. We are presently working on a dedicated LIA routine to correct FP observations interactively, which will require some inputs from the observer, as the astronomical source line shape and width. This will always make the correction observer-dependent.

Next: 6.10 Detector Non-linearity: the Up: 6. Caveats and Unexpected Previous: 6.8 `Detector Warm-up Features'

ISO Handbook Volume III (LWS), Version 2.1, SAI/1999-057/Dc