next up previous contents index
Next: 2.6 The LWS Detectors Up: 2. Instrument Overview Previous: 2.4 The Grating Spectrometer


2.5 The Fabry-Pérot Spectrometers

The resolving power for the grating-only mode was typically $\sim$200. To enhance this, Fabry-Pérot (FP) etalons were used to further select only a narrow portion of the spectrum within the grating passband. Although inherently capable of very high resolving power $(10^4-10^5)$ the FP interferometers, as used in ISO, were limited by the grating performance (see Figure 2.5) and by the ohmic losses in the FP plates, as discussed below.

An FP consists of two parallel partially reflecting plates between which multiple reflection occurs, creating constructive interference for the transmitted beam.

Figure 2.9: The construction of a Fabry-Pérot etalon.
\resizebox {12cm}{!}{\includegraphics[138,296][457,545]{fp_etalon.ps}}

The construction of the Fabry-Pérot etalons is shown in Figure 2.9. The Moving Plate is suspended on Leaf-Springs between the Back Plate and the Fixed Plate. Each corner of the moving plate carries a loudspeaker-like Drive Coil which operates in a gap surrounding a permanent magnet in the Back Plate. The position of each corner, relative to the Fixed Plate, is determined by measuring the charge on the Capacitance Micrometer, formed by pads on the Moving and Fixed Plates. The position of each corner is controlled by a servo-mechanism which supplies sufficient current to the Drive Coil to make the measured charge equal to a control value. Initially, the two plates of the etalon are made parallel by applying offset signals to two of the three drive circuits. The moving etalon is then scanned as a whole by applying the same additional driving signal to all three coils.

The fixed and moving plates carry the reflecting elements, made of free-standing nickel meshes supplied by Heidenhain: these meshes are affixed to the Mesh-Mounting Frames which are attached to the plates. The meshes consist of a rectangular grid of rectangular section: the thickness of the meshes is 3$\mu $m, the width of the `bars' of which the meshes are composed is 6$\mu $m, and the periods of the grid are 19$\mu $m for the long wavelength Fabry-Pérot and 15.5$\mu $m for the short wavelength Fabry-Pérot. The narrow tolerance allowed on these dimensions is critical to the performance of the instrument.

For monochromatic input, the transmitted intensity, $T_{\rm r}(\lambda,d)$, has a series of maxima dependent on the wavelength, $\lambda$, and plate separation, $d$, as prescribed by the function (Born & Wolf 1970, [1]):


\begin{displaymath} T_{\rm r}(\lambda ,d)=\frac{{\mathcal T}^2}{(1-{\mathcal R})^2+ 4{\mathcal R}^2\sin^2(\delta/2)}\ , \end{displaymath} (2.2)

where $\delta$ is the phase difference between adjacent transmitted rays and ${\mathcal R}$ and ${\mathcal T}$ are the single plate reflected and transmitted intensities respectively. This can be simplified by defining the parameter $F$ such that:


\begin{displaymath} F=\frac{4{\mathcal R}}{(1-{\mathcal R})^2}\ , \end{displaymath} (2.3)

giving:


\begin{displaymath} T_{\rm r}(\lambda,d)=\frac{{\mathcal T}^2}{(1-{\mathcal R})^2}\frac{1}{(1+F\sin ^2(\frac{\delta}{2}))} \end{displaymath} (2.4)

To take into account the intensity absorbed by the plates, ${\mathcal A}$, we apply:


\begin{displaymath} {\mathcal R}+{\mathcal T}+{\mathcal A}=1 \end{displaymath} (2.5)

Now using Equation 2.5 in Equation 6.2 and rearranging we have:


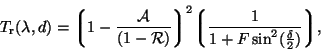\begin{displaymath} T_{\rm r}(\lambda,d)=\bigg\lgroup 1-\frac{\mathcal{A}}{(1-... ...igg\lgroup\frac{1}{1+F\sin ^2(\frac{\delta}{2})}\bigg\rgroup, \end{displaymath} (2.6)

where the first term on the right hand side expresses the wavelength dependent FP efficiency and the second factor is called the Airy Function.

The sharpness of the fringes is given by the Full Width Half Maximum (FWHM). A useful parameter to use is the reflective finesse, $\mathcal{F}$, which is the ratio of the separation of successive orders divided by the FWHM of the transmitted peaks. Using this definition and writing the phase difference of the $m$$^{th}$ peak as $\delta=2m\pi \pm \frac{\epsilon}{2}$ where $\epsilon$ is the phase shift from the line peak to its half power point, we see that:


\begin{displaymath} {\mathcal F}=\frac{\pi \sqrt{F}}{2}=\frac{\pi \sqrt{\mathcal R}} {1-{\mathcal R}} \end{displaymath} (2.7)

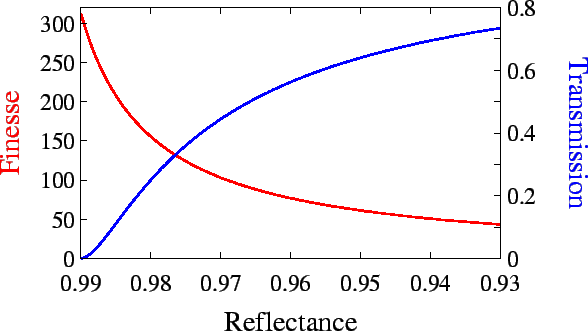
For a high resolving power, a finesse as large as possible was required. However, measurements by Davis et al. 1995, [12] indicate that the plate absorption was $\sim$1%. As can be seen from Figure 2.10, for a 1% absorption and 97% reflectance (which corresponds to a finesse of 100), the transmission is 44%. Increasing the reflectivity to 98% increases the resolving power but decreases the transmission to 25%. For 99% reflectivity (and 1% absorption) the finesse is very high, 312, however there is very little transmission.

Figure 2.10: FP finesse (red) and transmission (blue) as a function of reflectance for an absorption of 1%.
\resizebox {13cm}{!}{\includegraphics{transmission.eps}}

With metal mesh reflection plates, the reflectivity is wavelength dependent (Davis et al. 1995, [12]). Typically the reflectivity changes from about 0.96 to 0.98 for a frequency change of a factor of two. It is therefore impossible to cover the whole LWS range with both high finesse and good transmission. For this reason two FPs were used in the LWS: The Short wavelength FP (FPS) to cover the wavelength range of 47-70$\mu $m and the Long wavelength FP (FPL) for the range 70-196.6$\mu $m.

In wavenumber space, evenly separated peaks are produced by an FP. To avoid spectral contamination it was required that when a particular order is scanned across the grating response function of width $\Delta \sigma$, by varying the plate separation, $d$, no other FP orders would overlap with it (shown at the bottom of Figure 2.5). So for orders separated by $\Delta \sigma$ wavenumbers it is required that the distance between the two meshes is:


\begin{displaymath} d \leq \frac{1}{2 \Delta \sigma} \end{displaymath} (2.8)

Since the grating resolving power is constant in wavelength terms, the criterion for setting the FP gaps ($d$) needs to be determined for the shortest wavelength observed. The wavelengths of 45$\mu $m (222cm$^{-1}$) and 90$\mu $m (111cm$^{-1}$) were used2.1 for FPS and FPL, respectively. The spectral resolution of the grating in wavenumber units is 2cm$^{-1}$ and 1cm$^{-1}$ respectively at the short wavelength extremes of FPS and FPL. This results in a basic mesh separation of 2.7mm for FPS and 5.0mm for FPL from Equation 2.8. The actual motion required to scan the whole LWS range using the ten detectors was reduced to a small interval of $\sim$$d/n$, the displacement required to move the $n^{\rm th}$ peak to the $(n+1)^{\rm th}$ peak. For the LWS this was at most $\sim$35$\mu $m for FPS and $\sim$100$\mu $m for FPL.

The order of radiation at wavelength $\lambda_1$ is found from $d=\frac{n\lambda_1}{2}$, so that:


\begin{displaymath} n=\frac{2d}{\lambda_1}\ , \end{displaymath} (2.9)

hence at their shortest operational wavelengths FPS was used in the 120$^{\mbox{th}}$ and FPL in 111$^{\mbox{th}}$ order. At their longest wavelengths they worked in orders 77 and 50 for FPS and FPL respectively. This gave a range in resolving power for the FP of $\sim$5000 to 12000.

Other factors can limit the resolving power of an FP, such as the Jacquinot criterion (a limit induced by imperfect collimation), flatness criterion (limited by imperfect flatness of the plates) and even non-parallelism between the plates. All of these factors were made to be small, compared to the basic wire grid limitations discussed above.

The bottom panel of Figure 2.5 shows the expanded range for one particular grating setting for SW4 with the FPS in the beam. With the grating at an angle of $-1.36^{\circ}$, radiation of a wavelength 73.5$\mu $m falls on SW4. The Fabry-Pérot etalons could be scanned such that any spectral region within the grating bandwidth can be selected without contamination from higher or lower FP orders. A high resolution scan therefore required that the grating was stepped across the range of SW4 and within each step the FP was scanned across the grating spectral band. High resolution observations of the first order wavelengths were made in the same way, but using FPL with detectors LW1-5.
In this mode it was only possible in principle to use the output from one detector at a time, since it would be unlikely that the FP position and the grating position would be correct for any of the other four detectors in the FPS range2.2. It is therefore apparent that the LWS was very efficient when recording medium spectral resolution with the grating, but inefficient when observing the whole spectrum at high resolution. Indeed, for line work using the Fabry-Pérots, most scans were performed just around the known lines, which were evident from the grating spectra.

next up previous contents index
Next: 2.6 The LWS Detectors Up: 2. Instrument Overview Previous: 2.4 The Grating Spectrometer
ISO Handbook Volume III (LWS), Version 2.1, SAI/1999-057/Dc