next up previous contents index
Next: B. Magnitude System in Up: cam_hb Previous: 9.3 Interactive Data Processing


A. Colour Corrections

The transmission of optics and filters, as well as the quantum efficiencies of the detectors exhibit non-flat spectral dependencies. As a consequence, two sources radiating the same power within a given wavelength range but with different spectral shapes, produce two different signals. The flux density derived from measurements of a source in a given filter has to be corrected for this effect. Therefore the flux density at the reference wavelength of a certain filter of the broad-band photometry of ISOCAM has been computed for an a priori assumed spectral shape, a $F_\lambda(\lambda) \sim \lambda^{-1}$ law. This is the spectral density distribution which has the same shape for $F_\lambda(\lambda)$ and $F_\nu(\nu)$, namely $F_\lambda(\lambda) \sim \lambda^{-1}$ and $F_\nu(\nu)\sim \nu^{-1}$. The same convention was adopted for the flux densities quoted in the IRAS catalogues. Although this is an arbitrary choice, this does not imply any loss of generality, because the `real' flux density can be recovered by the colour correction described hereafter. In the CCG*WSPEC CAL-G files the spectral transmission curve for each filter is given. The spectral transmission $R(\lambda )$ as defined for ISOCAM is the product of the filter transmission $T(\lambda)$ and the detector quantum efficiency $Q(\lambda)$:


\begin{displaymath}R(\lambda) = T(\lambda) \times Q(\lambda) \end{displaymath}

No transmission curve for the lenses has been included. To determine the actual flux density one has to divide the flux density (derived after dividing the measured ADU/G/s by the SENSITIV parameter of the CCG*WSPEC CAL-G files) by the colour correction factor $K(\lambda_{\rm ref})$.


\begin{displaymath}F_{\rm actual} (\lambda_{\rm ref})=F_{\rm derived} / K(\lambda_{\rm ref})\end{displaymath}

where $K(\lambda_{\rm ref})$ is given by:


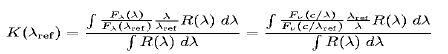\begin{displaymath} K(\lambda_{\rm ref})= \frac{\int \frac{F_\lambda(\lambda)}{... ...{\lambda} R(\lambda) \;d\lambda} {\int R(\lambda) \;d\lambda} \end{displaymath} (A.1)

The spectral transmission $R(\lambda )$ of the SW and LW channels of ISOCAM are shown in Figure A.1 and Figure A.2, respectively. Colour corrections calculated for different blackbody temperatures and for different power-laws ( $F_\nu \sim \lambda^{-\alpha}$) are shown in Tables A.1 - A.4.

Figure A.1: Spectral transmission $R(\lambda )$ of the SW channel of ISOCAM.
\resizebox {15cm}{9cm}{\includegraphics{filter_sw.ps}}

Figure A.2: Spectral transmission $R(\lambda )$ of the LW channel of ISOCAM.
\resizebox {15cm}{9cm}{\includegraphics{filter_lw.ps}}


Table A.1: Colour correction values for LW filters for different blackbody temperatures.
Temp LW1 LW2 LW3 LW4 LW5 LW6 LW7 LW8 LW9 LW10
10000 1.03 1.08 1.03 1.02 1.01 1.02 1.01 1.00 1.01 1.29
5000 1.02 1.07 1.03 1.02 1.01 1.00 1.01 1.00 1.01 1.27
4000 1.02 1.06 1.02 1.01 1.01 1.00 1.01 1.00 1.01 1.27
3000 1.02 1.05 1.03 1.01 1.01 1.00 1.01 1.00 1.01 1.26
2000 1.01 1.04 1.02 1.01 1.01 1.00 1.01 1.00 1.00 1.23
1000 1.00 0.99 1.01 1.00 1.00 0.99 1.00 1.00 1.00 1.17
800 0.99 0.98 1.01 1.00 1.00 0.99 1.00 1.00 1.00 1.13
600 0.99 0.96 1.00 0.99 1.00 0.99 0.99 1.00 1.00 1.08
400 1.01 0.98 0.99 1.00 1.00 1.00 0.99 1.00 1.00 1.00
300 1.06 1.06 0.98 1.01 1.00 1.01 0.99 1.00 1.00 0.94
250 1.12 1.17 0.98 1.04 1.00 1.03 1.00 1.00 1.00 0.91
200 1.26 1.43 0.99 1.09 1.00 1.06 1.03 1.00 1.00 0.91
150 1.65 2.18 1.02 1.24 1.02 1.16 1.11 1.02 1.00 0.96
100 3.30 6.23 1.20 1.78 1.09 1.51 1.42 1.06 1.02 1.30


Table A.2: Colour correction values for LW filters for different power laws ( $F_\nu \sim \lambda^{-\alpha}$). Note that the spectral index $\alpha=-1$ gives the `a priori' assumed spectrum ( $F_\nu(\nu)\sim \nu^{-1}$) and the colour correction is thus unity at all wavelengths.
$\alpha$ LW1 LW2 LW3 LW4 LW5 LW6 LW7 LW8 LW9 LW10
3.0 1.05 1.17 1.07 1.03 1.01 1.01 1.03 1.00 1.01 1.50
2.5 1.04 1.12 1.05 1.03 1.01 1.01 1.02 1.00 1.01 1.39
2.0 1.03 1.09 1.03 1.02 1.01 1.00 1.01 1.00 1.01 1.30
1.5 1.02 1.05 1.02 1.01 1.01 1.00 1.01 1.00 1.00 1.22
1.0 1.01 1.03 1.01 1.01 1.01 1.00 1.00 1.00 1.00 1.15
0.5 1.01 1.01 1.00 1.01 1.00 1.00 1.00 1.00 1.00 1.10
0.0 1.01 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.06
$-$0.5 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.02
$-$1.0 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
$-$1.5 1.00 1.01 1.01 1.00 1.00 1.00 1.00 1.00 1.00 0.98
$-$2.0 1.00 1.02 1.01 1.00 1.00 1.01 1.01 1.00 1.00 0.97
$-$2.5 1.00 1.04 1.02 1.00 1.00 1.01 1.01 1.00 1.00 0.97
$-$3.0 1.00 1.06 1.04 1.01 1.00 1.02 1.02 1.01 1.00 0.97


Table A.3: Colour correction values for SW filters for different blackbody temperatures.
Temp SW1 SW2 SW3 SW4 SW5 SW6 SW7 SW8 SW9 SW10 SW11
10000 1.05 1.00 1.07 1.03 1.04 1.01 0.96 1.00 1.02 0.98 1.03
5000 1.04 1.00 1.06 1.03 1.02 1.01 0.97 1.00 1.02 0.99 1.03
4000 1.04 1.00 1.06 1.03 1.02 1.01 0.97 1.00 1.02 0.99 1.02
3000 1.03 1.00 1.05 1.02 1.01 1.00 0.97 1.00 1.02 0.99 1.02
2000 1.02 1.00 1.04 1.01 0.99 1.00 0.98 1.00 1.01 0.99 1.02
1000 0.99 1.00 1.00 0.98 0.96 1.00 1.01 1.00 1.00 0.99 1.00
800 0.98 1.00 0.99 0.98 0.97 1.00 1.03 1.00 0.99 1.00 1.00
600 0.99 1.01 0.97 0.98 1.01 1.00 1.06 1.00 0.99 1.01 0.99
400 1.06 1.02 0.96 1.04 1.27 1.02 1.15 1.01 0.97 1.03 0.96
300 1.21 1.05 0.97 1.14 1.80 1.06 1.26 1.01 0.97 1.06 0.94
250 1.40 1.07 1.01 1.27 2.53 1.11 1.38 1.02 0.97 1.08 0.93
200 1.84 1.12 1.11 1.56 4.53 1.22 1.59 1.03 0.98 1.14 0.92
150 3.23 1.25 1.39 2.36 13.54 1.50 2.10 1.06 1.03 1.24 0.91
100 13.52 1.66 2.68 6.54 - 2.78 4.17 1.16 1.39 1.59 0.91


Table A.4: Colour correction values for SW filters for different power laws ( $F_\nu \sim \lambda^{-\alpha}$). Note that the spectral index $\alpha=-1$ gives the `a priori' assumed spectrum ( $F_\nu(\nu)\sim \nu^{-1}$) and the colour correction is thus unity at all wavelengths.
$\alpha$ SW1 SW2 SW3 SW4 SW5 SW6 SW7 SW8 SW9 SW10 SW11
3.0 1.09 1.00 1.11 1.06 1.12 1.02 0.95 1.00 1.03 0.98 1.04
2.5 1.07 1.00 1.09 1.05 1.08 1.01 0.96 1.00 1.03 0.98 1.03
2.0 1.06 1.00 1.08 1.04 1.05 1.01 0.96 1.00 1.02 0.98 1.03
1.5 1.04 1.00 1.06 1.03 1.03 1.01 0.97 1.00 1.02 0.99 1.02
1.0 1.03 1.00 1.04 1.02 1.01 1.00 0.97 1.00 1.01 0.99 1.02
0.5 1.02 1.00 1.03 1.02 1.00 1.00 0.98 1.00 1.01 0.99 1.01
0.0 1.01 1.00 1.02 1.01 0.99 1.00 0.99 1.00 1.01 0.99 1.01
$-$0.5 1.00 1.00 1.01 1.00 0.99 1.00 0.99 1.00 1.00 1.00 1.00
$-$1.0 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00
$-$1.5 1.00 1.00 0.99 1.00 1.01 1.00 1.01 1.00 1.00 1.00 1.00
$-$2.0 1.00 1.00 0.99 0.99 1.03 1.00 1.01 1.00 0.99 1.01 0.99
$-$2.5 1.00 1.00 0.98 0.99 1.06 1.00 1.02 1.00 0.99 1.01 0.99
$-$3.0 1.00 1.00 0.98 0.99 1.09 1.00 1.03 1.00 0.99 1.02 0.98

next up previous contents index
Next: B. Magnitude System in Up: cam_hb Previous: 9.3 Interactive Data Processing
ISO Handbook Volume II (CAM), Version 2.0, SAI/1999-057/Dc