Next: 4.11 Astrometric Uncertainties Up: 4. Calibration and Performance Previous: 4.9 Ghosts and Straylight

4.10 Field of View Distortion

ISOCAM images suffer from a field distortion caused by optical elements like the field mirror, filter and lens. Each of these elements acts in a different way and to a different extent. The inclination of the Fabry field mirror causes a trapezoidal deformation observed in the distortion pattern. This effect is reproduced in a simple first order optical computation. Pincushion distortion occurs when the beam passes through the lens and is caused by the aspherical aberration of the lens. In this case, first order computation is not sufficient to account for the effect. The width of the filter plates contribute also in a magnification change. As the beam is converging when passing through the filter, the parallel planes of the filter plates (whether inclined or not) have an influence on the field pattern on the detector. 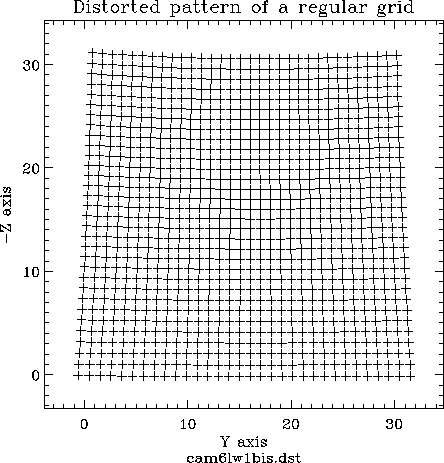An example of a field distortion pattern derived from a raster observation through the 6 $^{\prime \prime }$ pfov lens with the LW1 filter is shown in Figure4.26. It is important to correct data for this instrumental effect, especially when making a coadded map from a raster observation and also when improved astrometry is needed. The correction is made by means of a pair of polynomials which relate the distorted two-dimensional space to a distortion-free two-dimensional space.

**Figure 4.26:** *A typical field distortion pattern derived from a raster observation through the 6 $^{\prime \prime }$ pfov lens with the LW1 filter*
$\resizebox {15cm}{!}{\includegraphics{dst6lw1.ps}}$

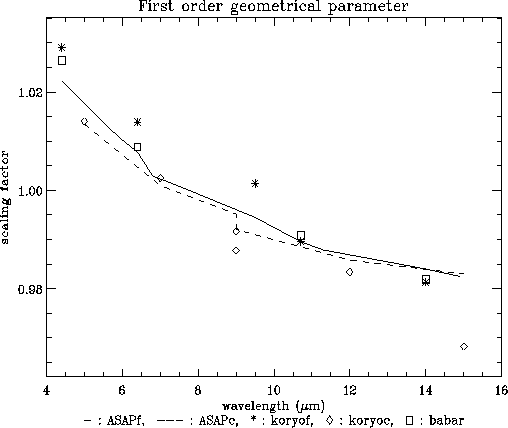
The distortion is weak through the 1.5 $^{\prime \prime }$ pfov lens and becomes stronger for larger pfov's. The field distortion also depends on the filter. Figure 4.27 shows the wavelength dependency seen in the data by means of the magnification parameter derived from the linear terms of the fit polynomials. The field distortion correction includes polynomial coefficient sets for the different filters. There are two types of coefficients. One derived from measurements and the other from a ray-tracing optical model which was optimised to fit the observations. Measurements on real data are possible in the case of the 6 $^{\prime \prime }$ and 12 $^{\prime \prime }$ pfov lenses. The distortion measurement through the 3 $^{\prime \prime }$ pfov lens was difficult because the effect which had to be measured was of the order of the accuracy of the point source position determination routine. The distortion amplitude is even smaller through the 1.5 $^{\prime \prime }$ lens, and is therefore impossible to measure in the real data. In CIA the distortion polynomial coefficients are available in a CAL-G file called `clwdisto_*.fits'. For the ISOCAM configurations for which no accurate measurement was possible or for which no data are available, the coefficients are derived from the optical model. A more detailed discussion on this subject can be found in the ISOCAM Field Distortion Report (Okumura 2000, [46]).

**Figure 4.27:** Scaling factor of the distortion correction polynomials with respect to the detector centre. $\ast$ : filters (from ghost measurements), $\diamond$ : CVFs (from ghost measurements), $\Box$ : new data sets. Solid line: filters model; dashed line: CVFs model (Okumura 2000, [46]).
$\resizebox {12cm}{9.5cm}{\includegraphics{distmagn.ps}}$

Next: 4.11 Astrometric Uncertainties Up: 4. Calibration and Performance Previous: 4.9 Ghosts and Straylight

ISO Handbook Volume II (CAM), Version 2.0, SAI/1999-057/Dc