Next: C.3 Colour Correction Values Up: C. Colour Corrections Previous: C.1 Application of Tabulated

C.2 Computation of Colour Correction Factors

C.2.1 Derivation of flux density values from in-band power values

In order to derive flux density values (monochromatic fluxes) from measured in-band powers the following corrections and calibrations have to be done:

a): correction for effective telescope area
b): correction for reflection losses on all optical elements in the beam from the primary mirror to the detector
c): correction for the beam profile related to the selected aperture or array
d): correction for the bandpass transmission, determined by the filter and field lens transmission and the relative detector response. The product of these factors is called the relative system response.

The latter correction contains the determination of the relative contribution of the flux density at the central wavelength of the band to the total flux in the band, depending on the assumed spectral shape of the source. Doing this calculation for a variety of source spectra and computing the ratios provides the colour correction factors between the various SEDs.

The flux conversion can be written in the following form:

$\begin{displaymath} IBP = T_{\rm refl} \cdot A \cdot \int f_{\rm beam}(\lambda) \cdot F(\lambda) \cdot R(\lambda)\,d\lambda \end{displaymath}$

(C.2)

where:


   = in-band power (unit: W)

   = reflection losses on optical elements

   = primary mirror area

   = wavelength dependent beam profile function

   = flux density of source at specific wavelength 

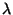
   = system response at specific wavelength

Currently the in-band power calculation contains some simplification, in particular related to the beam profiles.

For point source fluxes the following calculation is done:

$\begin{displaymath} IBP = T_{\rm refl} \cdot A \cdot f_{\rm psf}(\lambda_{\rm ref}) \cdot \int F(\lambda) \cdot R(\lambda)\,d\lambda \end{displaymath}$

(C.3)

where:


   = fraction of the point spread function at  the reference wavelength 

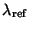
		   inside the aperture or pixel  Cal-G file PPPSF

For extended source fluxes the corresponding calculation is done:

$\begin{displaymath} IBP = T_{\rm refl} \cdot A \cdot (1-\varepsilon^{2}) \cdot \Omega \cdot \int F(\lambda) \cdot R(\lambda)\,d\lambda \end{displaymath}$

(C.4)

where:


   = central obscuration factor by the secondary mirror

   = solid angle of selected aperture or pixel

In order to derive the flux density for the central wavelength, or more general a reference wavelength, of the bandpass the spectral energy distribution function is normalised with respect to the flux density at this wavelength:

$\begin{displaymath} F(\lambda) = F(\lambda_{\rm ref}) \cdot \frac{SED(\lambda)}{SED(\lambda_{\rm ref})} \end{displaymath}$

(C.5)

where:


   = flux density at any wavelength 

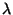
   = flux density at reference wavelength 

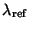
   = functional dependence of spectral energy distribution of   source with wavelength

Furthermore, for conversion between frequency range and wavelength range the following convention is used:

$\begin{displaymath} \lambda \cdot F(\lambda) = \nu \cdot F(\nu) \end{displaymath}$

(C.6)

where:


   = flux density in wavelength range (unit:   Wmm)

   = flux density in frequency range (unit: WmHz or   Jy)

Solving this equation for $F(\nu)$ yields:

$\begin{displaymath} F(\nu) = \frac{\lambda^{2}}{c_{\rm light}} \cdot F(\lambda) \end{displaymath}$

(C.7)

where:


   = speed of light

Using the normalisation with respect to the flux density value at the reference wavelength and the convention for conversion of $F(\lambda)$ into $F(\nu)$ the above formula of the in-band power can be solved for $F(\nu)$ for a general source energy distribution $SED(\lambda)$ :

$\begin{displaymath} F(\nu_{\rm ref}) = \frac{1}{b \cdot c_{\rm light}} \cdot \l... ...t \frac{IBP}{\int SED(\lambda) \cdot R(\lambda)\,d\lambda} \end{displaymath}$

(C.8)

where:

C.2.2 Flux density conversion factors for different spectral energy distributions

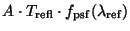
In the formula for the flux density $F(\nu)$ the term, which is dependent on the shape of the spectral energy distribution of the source, is called the flux density conversion factor

$\begin{displaymath} a(SED) = \frac{\lambda_{\rm ref}^{2} \cdot SED(\lambda_{\rm... ...rm light} \cdot \int SED(\lambda) \cdot R(\lambda)\,d\lambda} \end{displaymath}$

(C.9)

In the following the conversion factors for specific SEDs are listed:

1)

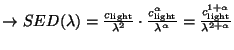
flux density $\propto \nu^{\alpha}, SED(\nu) = \nu^{\alpha}$ $\rightarrow SED(\lambda) = \frac{c_{\rm light}}{\lambda^{2}} \cdot \frac{c_{\r... ...lpha}}{\lambda^{\alpha}} = \frac{c_{\rm light}^{1+\alpha}}{\lambda^{2+\alpha}}$

$\begin{displaymath} a(\nu^{\alpha}) = \frac{1}{c_{\rm light} \cdot \lambda_{\r... ...\cdot \int \frac{R(\lambda)}{\lambda^{2+\alpha}}\,d\lambda} \end{displaymath}$

(C.10)

2)

flux density is a modified black body function with emissivity $\propto \nu^{\beta}, SED(\nu) = \nu^{\beta} \cdot B(\nu,T)$
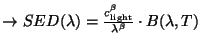$\rightarrow SED(\lambda) = \frac{c_{\rm light}^{\beta}}{\lambda^{\beta}} \cdot B(\lambda,T)$ ( $\beta = 0$ : pure black body)

$\begin{displaymath} a(\nu^{\beta} \cdot B(\nu,T)) = \frac{B(\lambda_{\rm ref},T... ...ac{B(\lambda,T)}{\lambda^{\beta}} \cdot R(\lambda)\,d\lambda} \end{displaymath}$

(C.11)

Note that:

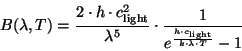$\begin{displaymath} B(\lambda,T) = \frac{2 \cdot h \cdot c_{\rm light}^{2}}{\la... ...^{\frac{h \cdot c_{\rm light}} {k \cdot \lambda \cdot T}}-1} \end{displaymath}$

(C.12)

where:


   = Planck constant

   = Boltzmann constant


B(,T) contains the  correction factor from the frequency  to wavelength conversion !

C.2.3 Derivation of colour correction factors from flux density conversion factors

From the general formula of the colour correction in Appendix C.1 it follows that

$\begin{displaymath} K_{\rm cc}(SED) = F_{\rm\nu_{\rm ref}}(\nu^{-1})~/~F_{\rm\nu_{\rm ref}} (SED) \end{displaymath}$

(C.13)

and with the formulae from Appendix C.2.1 for $F(\nu_{\rm ref})$

$\begin{displaymath} K_{\rm cc}(SED) = a(\nu^{-1})~/~a(SED) \end{displaymath}$

(C.14)

the colour correction factor is the ratio of the flux density conversion factors.

Inserting the formulae from Appendix C.2.2 for both flux density conversion factors this yields

$\begin{displaymath} K_{\rm cc}(SED) = \frac{1}{\lambda_{\rm ref} \cdot SED(\lam... ...mbda)\,d\lambda} {\int \frac{R(\lambda)}{\lambda}\,d\lambda} \end{displaymath}$

(C.15)

In order to calculate the colour correction factors this needs a numerical solution of the two integrals using the tabulated relative system response $R(\lambda_{\rm i})$ .

Next: C.3 Colour Correction Values Up: C. Colour Corrections Previous: C.1 Application of Tabulated

ISO Handbook Volume IV (PHT), Version 2.0.1, SAI/1999-069/Dc