Subsections

• 5.14.1 Prime mode observations coincident with parallel observations
• 5.14.2 Comparison with prime mode from stabilisation periods
• 5.14.3 Comparison between overlapping parallel rasters
• 5.14.4 Comparison with other instruments

5.14 Accuracy of the Parallel and Serendipity Mode Calibration

The calibration of the parallel and serendipity modes can be checked in various ways:

1. when the parallel data is taken at the same position as an independent prime pointing
2. before the instrument becomes prime there is some serendipity data at that pointing
3. by looking at overlapping parallel rasters taken on different revolutions

5.14.1 Prime mode observations coincident with parallel observations

Table 5.23 lists five L01 observations which were selected to provide a direct cross-check between parallel and prime mode. All L01 positions lie within the parallel rasters with the two Galactic Centre pointings being exactly coincident with one of the raster positions.

Figure 5.28 shows the Galactic Centre background position where the pointing is the same for the prime and parallel mode observations. For all positions the agreement is generally better than 20%. This result was obtained by comparing the fluxes from each detector at the parallel wavelengths with the prime data at those specific wavelengths. The best agreement was in the Galactic Centre position with the maximum flux. The first position in Oph, which is in a low flux region, showed the worst agreement. The uncertainties in dark current affect the quality of the data; hence, this result meets expectations. There were no systematic differences found, although detectors SW1 and SW2 could be more than a factor of two higher or lower than the prime mode. For the interpolated positions all other detectors were well within a factor of two of the prime mode.

Figure 5.28: The L01 full grating spectrum of a background position near the Galactic Centre. The diamonds are fluxes from an observation done in parallel mode at the same position.

Table 5.23: L01 observations concurrent with parallel observations.

TDT	RA	Dec	Source
29502313	16 25 43.5	24 11 39.8	Oph
48400517	16 27 02.0	24 37 25.6	Oph
29200534	16 26 26.3	24 24 29.9	Oph
69601005	17 48 00.8	28 37 38.1	Gal. Centre background
69600801	17 46 42.5	28 49 01.3	Gal. Centre

5.14.2 Comparison with prime mode from stabilisation periods

Before LWS prime mode observations are performed, there are between 10-20 ramps in the previous serendipity product, for which the on-target flag is OK, the pointing is stabilised and serendipity mode is still active. The fluxes obtained from these ramps can be compared to those obtained from the prime mode at the same grating position to check on how accurately the serendipity fluxes are being derived. In principle this can be done for every prime grating mode observation of a non-moving source. This check was performed on ten observations selected to have varying properties e.g. flux, source extent, etc. The agreement is very good when looking at bright point sources (see Figure 5.29; TDT 28701825) but less good when looking at bright extended sources (see Figure 5.29; TDT 28701401) and faint sources. It is also interesting to note that in the latter case, the LW2-LW4 detectors are saturated in prime mode and saturation effects are also present in the stabilisation period. The parallel flux is usually within 20% of the prime mode flux and there are no systematic deviations except for detector LW1 which was often about 30-40% lower in serendipity mode than in prime mode.

Figure 5.29: Two comparisons between serendipity mode just before an observation (filled diamonds) and averages at grating rest position during that observation (open diamonds).

5.14.3 Comparison between overlapping parallel rasters

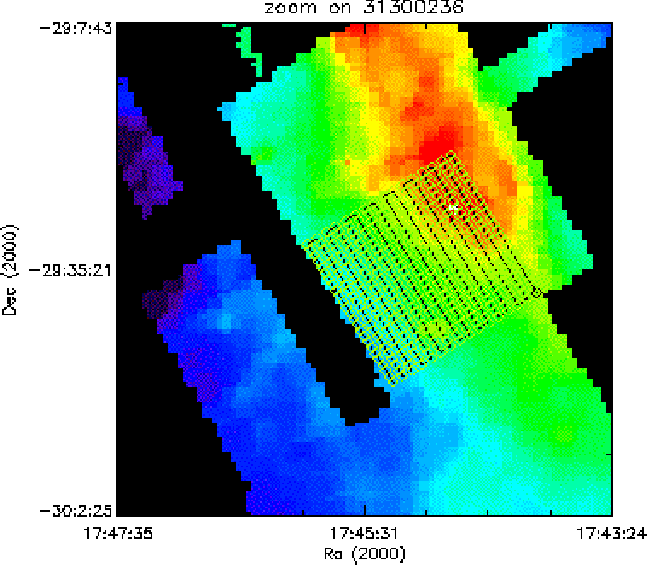
The parallel mode interactive analysis (LPIA) enables the building of a map from constituent product files using linear interpolation to form a uniform grid. Figure 5.30 shows one example where a map has been generated from about 15 large (30 points) rasters and 32 other parallel observations. The raster pointings superposed on this map are from TDT 31300236 and the fluxes obtained at each point, both in the map and the constituent raster are shown in Figure 5.31. Each individual point from the raster was ratioed with the nearest point in the map (i.e. for TDT 31300236, 401 ratios were obtained per detector) and these were averaged to get one comparison value for that detector per observation. This comparison was tried in three other areas (TDTs 32201917, 31201606 and 64102109) and the average ratio was always found to be within 20% with the majority of ratioes well within 10%.

Figure 5.30: A parallel map produced from several rasters in the Galactic Centre region. The pointings of one of the constituent raster observations, TDT 31300236, are shown.

Figure 5.31: The comparison between the map fluxes and the raster fluxes for the ten LWS detectors in the pointing sequence of TDT 31300236. The map fluxes are shown in blue and the raster fluxes are shown in red.

5.14.4 Comparison with other instruments

In addition to checking the internal calibration, comparisons can be made also with IRAS and ISOPHOT. For each of these other instruments the comparison is difficult to interpret as the flux obtained from LWS parallel observations covers a very narrow spectral band whereas the other instruments are observing a much broader spectral range. In spite of this, one important aspect which can be addressed by comparing LWS parallel data with data from other instruments, and which cannot be discerned with the internal checks, is to see if the beam shapes used for the conversion from to are reasonable. Maps were generated covering the Oph region and compared with IRAS High-Res maps, at m (with those of SW2 at m and SW3 at m) and m (with SW5 at 84.8 m, LW1 at m and LW2 at 122.1 m). The comparison was made by selecting linear strips across Oph and looking at the profiles along those strips. The difference between the instruments was no more than 10%. At m SW2 profiles almost exactly matched the IRAS profile and the SW3 profile was always higher indicating that the effective wavelength of the IRAS filter may be nearer the SW2 wavelength than SW3. At m LW1 gave a very good match (difference 5%) and SW5 (m) was higher, while LW2 (m) and the PHOT (-m) filter were lower. LW2 is the only detector in parallel mode where the wavelength is coincident with a strong ([N II]) line; therefore, we do not expect good agreement with IRAS as the IRAS m filter only has a 20% transmission at m.