In the following we will address only some general aspects related to the in-orbit performance of the ISO detectors. More details are given in the corresponding instrument specific volumes (II to V) of the ISO Handbook.
The performance of infrared detectors in space can be seriously affected by the ionising radiation environment. Charged particles can induce spikes (also known as `detector glitches'), higher dark current and detector noise as well as an increase level of responsivity.
The space radiation enviroment in which ISO was operated had four main constituents: geomagnetically trapped protons and electrons, solar protons and galactic cosmic rays (Nieminen 2001, [129]), each with a variable contribution depending both on the time of the mission and on the orbit phase.
The highly elliptic ISO orbit took the spacecraft deep into the Earth's
radiation belts in its perigee (![]() 1000 km) and to the interplanetary
space in its apogee (
1000 km) and to the interplanetary
space in its apogee (![]() 72000 km). To minimise the effect of
charged particles impacting the ISO detectors at low altitudes,
when the spacecraft crossed through the inner Van Allen belt (mainly
composed of high-energy protons), the on-board instruments were switched off
(see Section 4.2.2). At higher altitudes, during the ISO
science window, the spacecraft detectors were mainly affected by
galactic cosmic rays, but also by a significant number of
interplanetary and outer belt electrons. Additional effects can be
produced by electron bremsstrahlung in the outer structures of the
spacecraft and in the instrument shields, which may in turn give rise to
secondary electrons which can also hit the detectors. Actually, some
of the ISO instrument teams reported a clear correlation between detector
glitches and energetic electron fluxes as observed by the GOES-9 satellite
(Heras et al. 2001, [78]) especially
at the edges of the science window, i.e. at ISO altitudes comparable to that
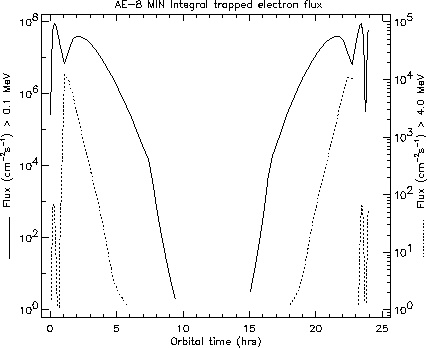
of GOES-9. Typical electron integral fluxes as a function of ISO orbital
time are shown in Figure 5.5 for two energy cut-offs.
72000 km). To minimise the effect of
charged particles impacting the ISO detectors at low altitudes,
when the spacecraft crossed through the inner Van Allen belt (mainly
composed of high-energy protons), the on-board instruments were switched off
(see Section 4.2.2). At higher altitudes, during the ISO
science window, the spacecraft detectors were mainly affected by
galactic cosmic rays, but also by a significant number of
interplanetary and outer belt electrons. Additional effects can be
produced by electron bremsstrahlung in the outer structures of the
spacecraft and in the instrument shields, which may in turn give rise to
secondary electrons which can also hit the detectors. Actually, some
of the ISO instrument teams reported a clear correlation between detector
glitches and energetic electron fluxes as observed by the GOES-9 satellite
(Heras et al. 2001, [78]) especially
at the edges of the science window, i.e. at ISO altitudes comparable to that
of GOES-9. Typical electron integral fluxes as a function of ISO orbital
time are shown in Figure 5.5 for two energy cut-offs.
|
On the other hand, since the ISO mission was
carried out nominally during the solar minimum period, the solar energetic
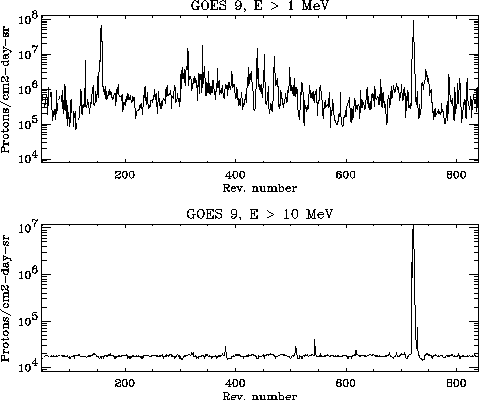
particle contribution was not significant, except for two moderate
solar proton events that took place towards the end of the mission: the
first, a double-event in November 1997 (revolutions 720-722) during wich
the proton flux for E![]() 10 MeV and E
10 MeV and E![]() 100 MeV increased by almost three
orders of magnitude and almost one order of magnitude respectively
with respect to its average value (see Figure 5.6);
and the second, shorter one in
April 1998, already during the so-called `Technology Test Phase' after
helium boil-off5.1.
The first event was clearly registered by all four ISO instruments (a
detailed description of the effects produced on the detectors
is given in Heras 2001, [77]), while
the second one had measurable effects on the ISO Star Tracker, as an
increased false count rate. Neither of these events contributed
significantly to the overall degradation of the satellite in comparison
with the long term effect of the constant radiation belt traversals.
100 MeV increased by almost three
orders of magnitude and almost one order of magnitude respectively
with respect to its average value (see Figure 5.6);
and the second, shorter one in
April 1998, already during the so-called `Technology Test Phase' after
helium boil-off5.1.
The first event was clearly registered by all four ISO instruments (a
detailed description of the effects produced on the detectors
is given in Heras 2001, [77]), while
the second one had measurable effects on the ISO Star Tracker, as an
increased false count rate. Neither of these events contributed
significantly to the overall degradation of the satellite in comparison
with the long term effect of the constant radiation belt traversals.
|
During the science observation window the
main source of radiation are galactic cosmic rays.
They originate outside the
solar system, and mainly consist of protons (85%), ![]() -particles
(14%), and a smaller component of heavier ions.
The major part of these particles cannot be stopped by the spacecraft
shielding since its differential spectrum peaks roughly between 500 MeV and
a few Gev, and are therefore highly penetrating.
Due to the high energies involved there is very little that can be done
to exclude these effects, and increasing the shielding thickness may in
fact be worse since more secondary particles (neutrons, protons,
spallation products) can be generated, thus potentially adding to the
problem (Nieminen 2001, [129]). The flux of cosmic rays
is anticorrelated with the solar activity. This is because
during the solar maximum period the expanding heliospheric magnetic field
scatters more effectively the arriving charged particles. Apart from the
slow variation over the solar cycle (not more than a factor of two in the
integral proton fluxes) this radiation environment component is very stable.
-particles
(14%), and a smaller component of heavier ions.
The major part of these particles cannot be stopped by the spacecraft
shielding since its differential spectrum peaks roughly between 500 MeV and
a few Gev, and are therefore highly penetrating.
Due to the high energies involved there is very little that can be done
to exclude these effects, and increasing the shielding thickness may in
fact be worse since more secondary particles (neutrons, protons,
spallation products) can be generated, thus potentially adding to the
problem (Nieminen 2001, [129]). The flux of cosmic rays
is anticorrelated with the solar activity. This is because
during the solar maximum period the expanding heliospheric magnetic field
scatters more effectively the arriving charged particles. Apart from the
slow variation over the solar cycle (not more than a factor of two in the
integral proton fluxes) this radiation environment component is very stable.
The main effect produced in the detectors by the space radiation environment is the production of signal spikes or `glitches' caused by particle hits in the detectors. They can have negative or positive polarity and any amplitude between telemetry resolution and saturation.
The detector `background' resulting from the steady cosmic ray bombardment in the science windows, as well as by the energetic electron fluxes in the Earth's radiation belt and/or from their secondaries form the bulk of the glitches analysed by the four instrument teams.
Upon impinging on the spacecraft, the incident particles can undergo
various processes that lead to a modification of the radiation environment
as seen at the instrument level. The highly energetic galactic cosmic rays
and solar event protons that reach the detectors even after thick shielding
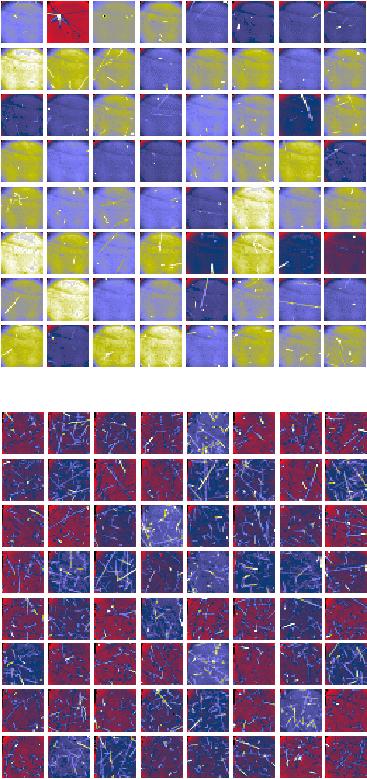
leave a trace of ionisation along their track. This can be clearly observed
as lines and spots in the detector pixel image, such as in the case of
ISOCAM (see Figure 5.7, analysis done by Sauvage 1997,
[143]). Numerous secondary particles such as ![]() -rays
and neutrons can also be generated, leading to shower-type particle cascades.
-rays
and neutrons can also be generated, leading to shower-type particle cascades.
|
With the minimum shielding of 9 mm Aluminum equivalent, electrons in the
outer radiation belt need energies of at least ![]() 4 MeV to reach any of
the ISO detectors. However, in slowing down in the shielding, the electrons
generate bremsstrahlung photons that can be more penetrating that
the incident electrons themselves. These electrons and photons may then be
observed as an increase in the low-energy part of the glitch spectrum.
The average energy deposited by a secondary electron, emitted on absorption
of a bremsstrahlung photon is 0.1-0.2 MeV in Si and
4 MeV to reach any of
the ISO detectors. However, in slowing down in the shielding, the electrons
generate bremsstrahlung photons that can be more penetrating that
the incident electrons themselves. These electrons and photons may then be
observed as an increase in the low-energy part of the glitch spectrum.
The average energy deposited by a secondary electron, emitted on absorption
of a bremsstrahlung photon is 0.1-0.2 MeV in Si and ![]() 0.1 MeV in
Ge.
0.1 MeV in
Ge.
Table 5.2 displays the glitch rates per unit area for the different ISO detectors as measured in-orbit. The results show that when comparing values for the same detector material, the observed glitch rates agree within a factor of 2-3.
| Detector type/ | Glitch rate | Minimum deposited energy |
| Instrument | [cm |
[keV] |
| Si:Ga | ||
| CAM | 14.9 | - |
| PHT-P1 | 6.5 | 1 |
| PHT-S | 5.8 | 1 |
| SWS | 10.0 | 1 |
| Ge:Be | ||
| LWS | 6.3 | 1.9 |
| SWS | 17.8 | 0.95 |
| SWS-FP | 10.1 | 0.95 |
| Ge:Ga | ||
| PHT-P3 | 10.1 | 1 |
| PHT-C100 | 12.5 | 1 |
| LWS | 7.0 | 1.2 |
| PHT-C200 (stressed) | 7.3 | 1 |
| LWS (stressed) | 6.7 | 1.3 |
The same analysis can be made for the observed glitch height (deposited energy) distributions. Again, the results obtained are consistent for detectors made of the same material (Heras 2001, [77]).
Considering the diversity of instrument designs, instrumental data and software used, the differences found can be attributed to: i) instrument shielding; ii) cross-talk between detectors, iii) the efficiency in the detection of small glitches, which is particularly important because they are the most numerous; iv) the uncertainty in the values of the photoconductive gain (especially for LWS), which affects the conversion from voltage jumps to energy deposited in the detectors; and v) the number of undetected glitches due to saturation.
Glitch rates per unit area and glitch height (energy deposited) distributions can also be predicted for the different ISO instruments and detectors with the help of Monte-Carlo simulations based on ray-tracing techniques or with full simulations of the physical processes ocurring along the track of the incident particles and their secondary particles, taking into account also the local shielding (this second approach was only needed for LWS since for the other three instruments the ray-tracing method provided a fair agreement with in-flight data). A detailed description of the results obtained from these simulations can be found in Heras 2001, [77] and references therein.
The comparison of the observed
energy deposited distributions with the results of ray-tracing
simulations which model primary cosmic ray-induced glitches only shows
a good agreement at high energies, but the peak of the observed distributions
at the lowest deposited energies are not reproduced,
especially in the Ge:Be detectors. In addition, the observed glitch rates
are between 1.5 and 4 times higher than the predicted values.
These facts, together with the
correlation found between glitch rates and the electron flux measured by the
GOES-9 spacecraft, lead to
the conclusion that between 30 and 75% of the observed glitches are caused
by ![]() -rays and other secondary particles produced by
cosmic rays and the environment protons and electrons
in the detectors and in the instrument and satellite shields
(Heras et al. 2001, [78]).
-rays and other secondary particles produced by
cosmic rays and the environment protons and electrons
in the detectors and in the instrument and satellite shields
(Heras et al. 2001, [78]).
Glitches were detected and removed from ISO data following deglitching algorithms implemented in the ISO Off-Line Processing pipeline. In some cases more sophisticated deglitching methods have been provided in the Interactive Analysis software packages. They are described in detail in Heras 2001, [77] and references therein, or in the instrument specific volumes (II to V) of this Handbook and, thus, will not be discussed here.
Although radiation effects are mainly recognised by the presence of glitches in the science data, in some cases they are also associated with temporal changes in detector responsivity, dark current levels and noise.
SWS:
The space radiation environment affected the long term behaviour of
band 3 Si:As SWS detectors, causing their dark current levels, and in some
cases, their dark current noise, to increase during the mission. The other
SWS detector bands were stable and did not show long term trends.
Some of the worse band 3 detectors cured spontaneously (e.g. detectors
34 and 36), that is, their dark currents and noise decreased suddenly
to launch levels without apparent reason. Laboratory tests in which
Si:As detectors were irradiated with 100 MeV protons during long periods
reproduced successfully the in-orbit behaviour. Although no curing procedure
could be found, it was decided to operate the detector at a lower bias
than initially planned, which reduced the damaging radiation effects
and kept the dark currents and noise at acceptable levels during the
mission (Heras et al. 2001, [78]).
LWS:
A similar behaviour was observed in LWS detectors.
Sudden voltage jumps produced by impacts affecting a given integration
ramp were followed by a change in the detector responsivity
in the following ramps. In addition to these `positive'
glitches, `negative' ones have also been found. These caused a sudden
decrease in the ramp voltage, and are thought to be produced by hits on
the FET. Negative glitches did not appear to affect the detector
responsivity (Swinyard et al. 2000, [156]).
The overall responsivity of the detectors increased with
particle hits during the orbit. To re-normalise the
responsivity, the bias current was increased beyond the breakdown voltage for
each detector twice in every orbit: a first bias boost on exit from
the Van Allen belts; and a second one half way through the 24 hour orbit.
Dark currents were not affected by the cosmic rays and remained
constant during an orbit. The change in responsivity between bias boosts was
monitored by the use of the infrared illuminators. This way it was possible
to correct for the overall drift in responsivity with time during an orbit
in the processing pipeline.
CAM:
In ISOCAM, responsivity variations were also detected after
perigee passage due to the very high radiation dose coming from trapped
particles in the Van Allen belts. In extensive radiation tests performed
before launch it was already found that ![]() -ray sources, protons and
heavy ions impacting the detectors induced a responsivity increase which
relaxed in a few hours. The effect was minimised if the photo-conductor
was polarised and exposed to a high infrared flux. In-orbit, during
the perigee passage, since the instrument was switched-off, a specific power
supply kept a bias voltage on the photo-conductors, and the camera was left
open to light. The responsivity variation often remained below 5% in
the science window. Appart from common glitches, other types of
glitches were detected in ISOCAM data and classified as: faders,
where the pixel value decreases slowly until a stabilised value is
reached (Figure 5.8); and
dippers, where the pixel value decreases first below the stabilised value,
and then increases slowly until the stabilised value is reached (see Figure
5.9). While common glitches are interpreted as
induced by both trapped and galactic protons and electrons, faders
would be induced by energetic protons, electrons and light galactic ions,
and dippers would be induced by heavy galactic ions (Claret et al.
2000, [25]). The effect of glitches are not so dramatic
for SW detectors as for LW detectors. This is
because the active zone of the pixel is very thin,
-ray sources, protons and
heavy ions impacting the detectors induced a responsivity increase which
relaxed in a few hours. The effect was minimised if the photo-conductor
was polarised and exposed to a high infrared flux. In-orbit, during
the perigee passage, since the instrument was switched-off, a specific power
supply kept a bias voltage on the photo-conductors, and the camera was left
open to light. The responsivity variation often remained below 5% in
the science window. Appart from common glitches, other types of
glitches were detected in ISOCAM data and classified as: faders,
where the pixel value decreases slowly until a stabilised value is
reached (Figure 5.8); and
dippers, where the pixel value decreases first below the stabilised value,
and then increases slowly until the stabilised value is reached (see Figure
5.9). While common glitches are interpreted as
induced by both trapped and galactic protons and electrons, faders
would be induced by energetic protons, electrons and light galactic ions,
and dippers would be induced by heavy galactic ions (Claret et al.
2000, [25]). The effect of glitches are not so dramatic
for SW detectors as for LW detectors. This is
because the active zone of the pixel is very thin, ![]() 10
10![]() m, so
that its volume is very small. Due to the very low energy needed to
create a free carrier pair, the charge generation is equivalent for
both SW and LW detectors, but the pixel geometry of the SW array
ensures that most of the particles cross only one pixel. After a hit
the responsivity of the pixel decays slowly to its previous value.
The decay time is the same as for transients due to IR flux
changes (see Section 5.6.2).
The lower the illumination of the array, the longer the decay time.
m, so
that its volume is very small. Due to the very low energy needed to
create a free carrier pair, the charge generation is equivalent for
both SW and LW detectors, but the pixel geometry of the SW array
ensures that most of the particles cross only one pixel. After a hit
the responsivity of the pixel decays slowly to its previous value.
The decay time is the same as for transients due to IR flux
changes (see Section 5.6.2).
The lower the illumination of the array, the longer the decay time.
![\resizebox {12cm}{5cm}{\includegraphics*[90,375][550,710]{fig_glitch_h1.ps}}](img120.gif)
|
![\resizebox {12cm}{6cm}{\includegraphics*[90,555][555,710]{dipper.ps}}](img121.gif)
|
PHT:
The continuous hits of high energy particles during the ISO orbit also
increased the responsivity of PHT detectors at short term and long term
scales. At short term scales the disturbance of an integration ramp after a
hit was usually followed by a tail-like signal excess lasting a few
integration ramps, which is interpreted as a momentary response variation.
At long term scales, already during the pre-flight calibration tests
it was found that the responsivity of the detectors
increased after exposing them to high energy radiation. The same
behaviour was found in-orbit, affecting mostly the
responsivity of the Ge-based, low bias voltage
far-infrared detectors (P3, C100 and C200), whereas the Si-based,
high bias voltage detectors P1, P2 and PHT-SS showed only small changes in
their responsivity. An exception was the
PHT-SL array which showed a similar, but less pronounced behaviour as the
FIR detectors. This change of responsivity was also found to be correlated
in-orbit with the geomagnetic activity and the electron fluxes, increasing
systematically (by 20-50%)
one or two days after the onset of a geomagnetic storm.
P3 and C100 showed the largest changes, followed by C200 (Castañeda
& Klaas 2000, [14]).
Due to the high radiation doses during perigee passage
the responsivities and noise levels of the ISOPHOT detectors were
strongly increased before the
beginning of every new science window. Therefore, appropriate curing
procedures were designed for the different detectors to restore the nominal
responsivities. The procedures were applied after the switch-on of the
instrument, before the beginning of the science window. For the doped
germanium detectors (P3, C100 and C200) they consisted of
a combination of bright IR-flashes using one of the FCSs and a bias boost
(absolute increase of the bias voltage). For the doped silicon detectors
(PHT-SS, PHT-SL, P1 and P2) curing was achieved by exposing the detector to
a higher temperature at a reduced bias voltage for a defined period of time.
In addition, P1 underwent an infrared flash curing.
The doped germanium detectors were much more susceptible to drifts caused
by accumulating effects of the high energy radiation impacts. In order to
keep their responsivities within the nominal range a second curing
procedure was applied around apogee passage in the handover window,
when the satellite control was switched from VILSPA (Madrid) to Goldstone
(California). Trend analysis performed immediately after the curing procedure
showed that the nominal responsivities were re-established with ![]() 2%
accuracy for all detectors, if the space environment conditions were stable.
On the other hand, low energy glitches also affected the measurements by
increasing the dark current level and the detector noise.
The consequence was an increase of the
minimum measurable signal, or equivalently, a decrease of the sensitivity
limit. All these effects are associated with the generation of
electron-hole pairs in the bulk of the detectors during the irradiation, and
with the capture of the minority carriers by the compensating impurities.
2%
accuracy for all detectors, if the space environment conditions were stable.
On the other hand, low energy glitches also affected the measurements by
increasing the dark current level and the detector noise.
The consequence was an increase of the
minimum measurable signal, or equivalently, a decrease of the sensitivity
limit. All these effects are associated with the generation of
electron-hole pairs in the bulk of the detectors during the irradiation, and
with the capture of the minority carriers by the compensating impurities.
The operation of infrared detectors in space is strongly complicated by memory effects. These detectors are usually doped silicon and germanium bulks with implanted low ohmic contacts used as extrinsic photoconductors and are characterised by a transient response after flux changes.
A large number of such detectors were used on board ISO (see Table
5.3). From this point
of view, the ISO satellite was a very interesting laboratory since several
technologies and detector materials (Ge:Be, Ge:Ga, In:Sb, CID In:Sb, Si:As,
Si:Ga, Si:B) were used to cover a wide spectral range from 2.5 to 240
![]() m.
m.
| Detector Name | Type | Wavelength ( |
Pixels | |
| CAM | SW | CID In:Sb | 2.5 - 5.5 | |
| LW | Si:Ga | 4.0 - 18.0 | ||
| PHT | SS & SL | Si:Ga | 15, (peak) | 64 |
| P1 | Si:Ga | 15, (peak) | 1 | |
| P2 | Si:B | 25, (peak) | 1 | |
| P3 | Ge:Ga | 100, (peak) | ||
| C 100 | Ge:Ga | 100, (peak) | ||
| C 200 | Ge:Ga (stressed) | 180, (peak) | ||
| SWS | band 1 | In:Sb | 2.38 - 4.08 | |
| band 2 | Si:Ga | 4.08 - 12.0 | ||
| band 3 | Si:As | 12.0 - 29.0 | ||
| band 4 | Ge:Be | 29.0 - 45.2 | ||
| FP band 5 | Si:Sb | 11.4 - 26. | ||
| FP band 6 | Ge:Be | 26.0 - 44.5 | ||
| LWS | SW1 | Ge:Be | 43 - 51 | 1 detector |
| SW2-SW5, LW1 | Ge:Ga | 50 to 121 (10) | 5 detectors | |
| LW2-LW5 | Ge:Ga (stressed) | 108 to 197 (20) | 4 detectors |
Some of these detectors exhibit long time constants and it was usually not possible to wait for current stabilisation when they were exposed in space to sources of infrared emission, making the determination of the input fluxes a very difficult task. Without any correction, the errors induced by the transient effects can be as large as 50% in some cases. However, in some of the ISO detectors and under certain circumstances, the response after a flux change was highly reproducible, which gives sense to look for models and to correct the data for these transient effects.
Before launch, ground-based tests were extensively performed (CAM - Pérault et al. 1994, [136]; PHT - Groezinger et al. 1992, [65]; Schubert et al. 1994, [146]; Schubert 1995, [145]; SWS - Wensink et al. 1992, [164]). Unfortunately, as a result of these ground-based tests it was not possible to develope and accurate model for transients in SWS and CAM. Only for PHT-S a promising non-linear model was proposed (Fouks & Schubert 1995, [54]), that was later corrected to introduce the effect of temperature variations.
During the ISO mission, several linear and non-linear models were suggested for the various ISO instruments and observing modes. It became evident that the models should be non-linear and non-symmetrical and take into account the illumination history of the detector.
Analytical models were developed for infrared detectors by Vinokurov & Fouks 1991, [162], from the non-linear equations describing such detectors (Vinokurov & Fouks 1991, [162]; Haegel et al. 1999, [71]). One of these models, the so-called `Fouks-Schubert' model (Fouks & Schubert 1995, [54]), was the one used for describing transients in PHT-S detectors during the ground-based tests, as we have already mentioned. This is a simplified analytical model which is able to reproduce the behaviour of Si:Ga detectors which high accuracy.
The Fouks-Schubert model and the basic equations involved are described in
Coulais et al. 2000, [36], and references therein. The Fouks-Schubert formula, which describes the detector behaviour when starting from an unstabilised current ![]() at the end of block
at the end of block ![]() is:
is:
where the time ![]() is measured from an arbitrary instant after the flux change at time
is measured from an arbitrary instant after the flux change at time ![]() ,
, ![]() is the instantaneous jump and
is the instantaneous jump and ![]() is a constant. The unstabilised current
is a constant. The unstabilised current ![]() before the flux change reflects the history of the detector (stabilisation in block
before the flux change reflects the history of the detector (stabilisation in block ![]() is achieved when
is achieved when
![]() );
);
![]() is the steady-state current under
the constant incoming flux during block
is the steady-state current under
the constant incoming flux during block ![]() .
.
This simple non-linear analytical formula (Equation 5.2), which takes into account the memory effects, describe the processes in the detector bulk, with the use of Fouks' boundary condition (Fouks 1981a, [50]; 1981b, [51]) that describes the properties of the detector contacts. This boundary condition has the form:
where
![]() is the hole
concentration at the plane
is the hole
concentration at the plane ![]() measured from the injecting contact
placed at the plane
measured from the injecting contact
placed at the plane ![]() , the time
, the time ![]() is measured from an
arbitrary instant, as in Equation 5.2,
is measured from an
arbitrary instant, as in Equation 5.2,
![]() is the change of the near-contact field
with time (
is the change of the near-contact field
with time (
![]() ), and
), and
![]() is the injection ability of the contact.
Equation 5.3 allows to describe the contact properties with a
high precision (Fouks & Schubert 1995, [54]) and,
in addition, to take into consideration additional
technological and engineering effects inherent to real
detectors (Fouks 1997, [52]).
is the injection ability of the contact.
Equation 5.3 allows to describe the contact properties with a
high precision (Fouks & Schubert 1995, [54]) and,
in addition, to take into consideration additional
technological and engineering effects inherent to real
detectors (Fouks 1997, [52]).
The use of Equation 5.3, instead of a detailed consideration
of the processes which occur inside the
near-contact space-charge region, strongly simplifies the description of
transient currents. Nevertheless, in general the problem
remains rather complex even
after this simplification. However, in the case where ![]() is much less
than the steady-state field in the detector bulk
is much less
than the steady-state field in the detector bulk
![]() (where
(where ![]() is the
steady-state voltage applied to the detector,
is the
steady-state voltage applied to the detector, ![]() is the inter-contact
distance), this description can be additionally strongly simplified,
and Equation 5.2 serves as a very exact description for transient
currents (Vinokurov & Fouks 1991, [162]).
The parameter
is the inter-contact
distance), this description can be additionally strongly simplified,
and Equation 5.2 serves as a very exact description for transient
currents (Vinokurov & Fouks 1991, [162]).
The parameter ![]() quantifies the quality of the
contacts and depends on the flatness of the donor profile in the
near-contact region and is linked to the time constant of the current
relaxation. The higher the contact quality, the less is
quantifies the quality of the
contacts and depends on the flatness of the donor profile in the
near-contact region and is linked to the time constant of the current
relaxation. The higher the contact quality, the less is ![]() ,
and the shorter the time constant. In real detectors at liquid helium
temperatures
,
and the shorter the time constant. In real detectors at liquid helium
temperatures ![]() is of the order of 10
is of the order of 10![]() -10
-10![]() V/m.
For Si:Ga detectors
V/m.
For Si:Ga detectors ![]() is considerably high, typically
10
is considerably high, typically
10![]() -10
-10![]() V/m, which provides a very high accuracy
to Equation 5.2. In Ge:Ga detectors
V/m, which provides a very high accuracy
to Equation 5.2. In Ge:Ga detectors ![]() , however,
, however, ![]() is of
the order of
is of
the order of ![]() , thus making this formula not so exact.
, thus making this formula not so exact.
The other important point lies in the fact that Equation 5.2
is applicable only when the illumination is uniform on the pixel surface.
In this case,
high photoelectric non-stationary cross-talking between adjacent
pixels, that are inherent to such detectors (Fouks & Schubert 1995,
[54]),
compensate each other, which makes the electric field
uniform along the planes ![]() and the used one-dimensional equations true.
Under non-uniform illumination the set of one-dimensional
equations cannot be used, and
Equation 5.2 looses its accuracy (Vinokurov & Fouks 1988,
[161];
Vinokurov et al. 1992, [163]).
and the used one-dimensional equations true.
Under non-uniform illumination the set of one-dimensional
equations cannot be used, and
Equation 5.2 looses its accuracy (Vinokurov & Fouks 1988,
[161];
Vinokurov et al. 1992, [163]).
Several Si:Ga detectors were on board ISO (see Table
5.3): the LW 32![]() 32 matrix array of ISOCAM; the
band 2 (a 1
32 matrix array of ISOCAM; the
band 2 (a 1![]() 12 linear array) of SWS; and the PHT-SS, PHT-SL and
P1 detectors of ISOPHOT.
12 linear array) of SWS; and the PHT-SS, PHT-SL and
P1 detectors of ISOPHOT.
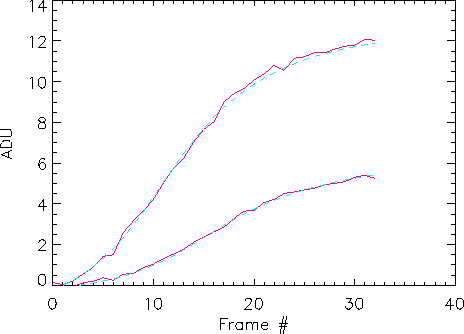
The LW detectors of ISOCAM present strong transient effects.
The worst situations occurred in two cases:
The transient behaviour of the LW channel has two main components
(see Figure 5.10):
a short term one which consists of
an initial jump typically of about 40-60% of
total signal step, followed by a long term drift with small
amplitude oscillations (typically 5-10![]() of the flux)
and can last hours (Abergel et al. 2000,
[1]; Coulais & Abergel 2000,
[35]).
of the flux)
and can last hours (Abergel et al. 2000,
[1]; Coulais & Abergel 2000,
[35]).
![\resizebox {11cm}{!}{
\includegraphics*[5,5][480,330]{fig1_transient_long.eps}}](img149.gif)
|
Upward and downward steps are not symmetrical (downward steps are hyperbolic-like) and the short term response at a given time strongly depends on the past of the observation and also on the spatial structure of the input sky (e.g. uniform emission or point sources).
Under quasi-uniform illumination the short term
transient response of individual LW pixels can be described by
the Fouks-Schubert model with an accuracy
around 1![]() per readout for all pixels except near the edges.
(Coulais & Abergel 2000, [35]). This model
is fully characterised by the two parameters (
per readout for all pixels except near the edges.
(Coulais & Abergel 2000, [35]). This model
is fully characterised by the two parameters (![]() ,
, ![]() ) above
mentioned, which are determined for each pixel in the array.
No significant changes of these parameters were observed during the
whole in-orbit ISO life per pixel, so that only one 32
) above
mentioned, which are determined for each pixel in the array.
No significant changes of these parameters were observed during the
whole in-orbit ISO life per pixel, so that only one 32![]() 32 map for
each
parameter was used when this correction was applied in the data reduction
pipeline. In addition, the dispersion found in the values derived
from pixel to pixel indicates that:
32 map for
each
parameter was used when this correction was applied in the data reduction
pipeline. In addition, the dispersion found in the values derived
from pixel to pixel indicates that:
In the LW array, the pixels are defined only by the electrical field
applied between the upper electrode and the bottom 32![]() 32 contacts.
As a consequence of the electrical design of the matrix array,
the adjacent pixels are always affected by cross-talk effects
(Vigroux et al. 1993, [160]).
Under uniform illumination these cross-talks compensate each other and
can be ignored but
this is not the case when the input sky contains strong fluctuations
with typical angular scale around the pixel size (e.g. point sources
with gradient between pixels typically higher than 20 ADU/s).
Thus, the one-dimensional Fouks-Schubert model fails for such point
sources, and three-dimensional models are required.
32 contacts.
As a consequence of the electrical design of the matrix array,
the adjacent pixels are always affected by cross-talk effects
(Vigroux et al. 1993, [160]).
Under uniform illumination these cross-talks compensate each other and
can be ignored but
this is not the case when the input sky contains strong fluctuations
with typical angular scale around the pixel size (e.g. point sources
with gradient between pixels typically higher than 20 ADU/s).
Thus, the one-dimensional Fouks-Schubert model fails for such point
sources, and three-dimensional models are required.
The LW-CAM data contained in the ISO Data Archive are corrected for transients using the `standard' one-dimensional Fouks-Schubert model above described. This means that the results obtained in fields with bright point sources or very steep gradients after applying this correction are not so accurate, although this is still within the few percent level.
Recently, a new simplified three-dimensional model for point source
transients has been
developed by Fouks & Coulais 2002, [53]. This
model uses the same (![]() ,
, ![]() ) parameters
which were used for the uniform illumination case and is able to
qualitatively reproduce real point source transients. The
model predicts e.g. that, starting
from the same initial level, the stronger the source the faster the
transient response and the higher the initial overshoot, as it is observed
in real data, and it works better for configurations in which the PSF is
narrow. A more
complicated three-dimensional model, able to account
for quantitative effects taking into account the true geometrical and
electrical specifities of LW detectors, is still under development
) parameters
which were used for the uniform illumination case and is able to
qualitatively reproduce real point source transients. The
model predicts e.g. that, starting
from the same initial level, the stronger the source the faster the
transient response and the higher the initial overshoot, as it is observed
in real data, and it works better for configurations in which the PSF is
narrow. A more
complicated three-dimensional model, able to account
for quantitative effects taking into account the true geometrical and
electrical specifities of LW detectors, is still under development
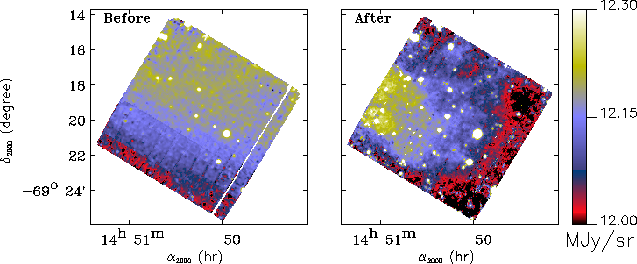
With respect to the remaining effects above mentioned (long term drift, small amplitude oscillations,..) no physical models exist yet to describe the detector behaviour and only empirical dedicated processing methods have been developed so far. Two approaches exist for the extraction of reliable information from raster observations affected by long term drifts. For the case of faint point sources, as in cosmological surveys, source extraction methods are discussed in Starck et al. 1999, [152] and Désert et al. 1999, [45]. For raster maps with low contrast large-scale structure (as in the case of diffuse interstellar clouds) a long term drift correction method is available in CIA. This method was developed by Miville-Deschênes et al. 1999, [121] and is based on the use of the spatial redundancy in raster observations to estimate and to correct for the long term drift (see Figure 5.11).
|
For ISOPHOT Si:Ga detectors (P1, PHT-SS and PHT-SL detectors),
and although a good agreement was achieved between transients and Fouks
models during ground-based tests, the application of these models to
real in-flight data was unsuccessful. Several facts can explain the change
in the behaviour of the detectors:
Typical drift curves in P1 detectors are shown in Figure 5.12. In case of a flux drop, a signal decay and in case of increasing flux steps, a signal rise is observed. In addition, a hook response during the first 40 seconds is also observed for large positive flux steps. The signal shows a behaviour similar to a strongly damped oscillation around the asymptotic level. For even higher flux steps the signal behaviour can be restricted to an overshoot followed by a slow decay. Doped silicon detectors tend to show a longer stabilisation time than doped germanium detectors (P3, C100 and C200 in the case of ISOPHOT), which can go from just a few seconds to hours. The relative stabilisation time is faster for positive flux steps. and steps at low flux levels take more time to stabilise. In addition, the stabilisation time also depends on the temperature of the detector.
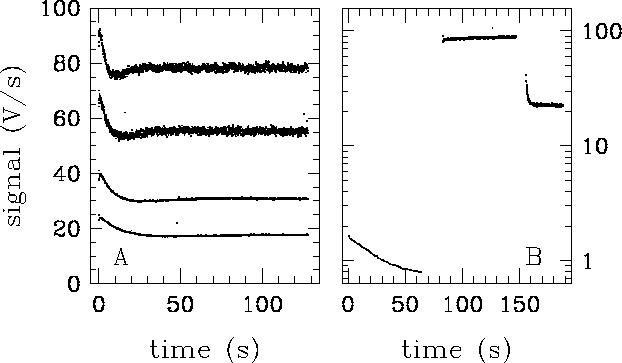
|
In OLP no sophisticated treatment of transients was applied to staring PHT-P1 observations. Instead, an algorithm was used which determines per chopper plateau whether a significant signal drift is present based on the application of the non-parametric Mann statistical test to the signals (Hartung 1991, [74]). In case such a drift is found, only the last stable part of the chopper plateau is used. Of course, this correction only works satisfactorily for measurements which are long compared to the stabilisation time. This `drift recognition' method is explained more in detail in Section 7.3 of the ISO Handbook Volume IV on ISOPHOT, [107].
In the case of chopped PHT-P1 observations, non-stabilised signals cause significant losses on the true difference signal. Signal derivation in OLP relies on the analysis of signals from pairs of consecutive readouts rather than signals per ramp. This gives better statistics of the signals per chopper plateau, since in many chopped measurements each chopper plateau covers only a few (typically 4) ramps. To increase further the robustness in determining the difference signal, the repeated pattern of off-source and on-source chopper plateaux is converted into a `generic pattern'. The generic pattern consists of only 1 off- and 1 on-source plateau and is generated using an outlier resistant averaging of all plateaux. The shape of the generic pattern determines the correction factors to apply with regard to stabilised staring measurements of a sample of calibration standards.
For PHT-S observations taken in staring mode an alternative approach was developed, known as the `dynamic calibration' method, which performs the calibration measurement by comparing the transient behaviour of the unknown source with that of celestial standards of similar brightness. Then, the transients which show the same time scale and amplitude for both measurements cancel out in the calibration process. This method works only for staring PHT-S observations because the flux history of PHT-S pixels is similar in all observations as they always start with a 32 s dark measurement which is followed by the real measurement. A detailed description of how the flux assignment is performed and the library of calibration standards and model spectra used for the application of this method can be found in García-Lario et al. 2001, [60]. The `dynamic calibration' brings down the errors associated to this observing mode (sometimes as high as 30%) to just a few percent.
Note that this accuracy is not applicable to raster measurements made with PHT-S, which also generally suffer from transient effects, because the assumption of a flux history similar to that used for the calibration stars is not met for all raster points in a map except for the first one. Thus, only a static spectral response function can be applied in this case. The photometric calibration of each raster point is performed by converting the signal to a flux using an average spectral response function for PHT-S staring observations derived from 40 observations of 4 different standard stars with different brightness.
The same argument is applicable to chopped PHT-S observations. Thus, for this observing mode a `drift recognition' routine similar to the one used for P1 detectors was implemented in OLP to detect the presence of a significant signal transient on a chopper plateau. When a transient is detected, a range of unreliable signals are flagged. The signal so derived is then corrected assuming a spectral response function corrected for chopper losses. The Fouks-Schubert model is not applicable in this case because the sources are usually very faint and the signal-to-noise ratio is too low for the fitting procedure to work properly. Thus, although the possibility exists in PIA of applying the Fouks-Schubert correction to faint sources observed in chopped mode, the above alternative approach was used to calibrate these sources in the automated pipeline. More details on the method applied and the calibration of the standard stars used for this purpose are given in García-Lario et al. 2001, [60].
An overview of the various transient behaviours observed for the different
SWS bands as a function of the detector material is shown in Figure
5.13, where we can see that band 2 (Si:Ga) and
band 4 (Ge:Be) are those affected by the largest memory effects.
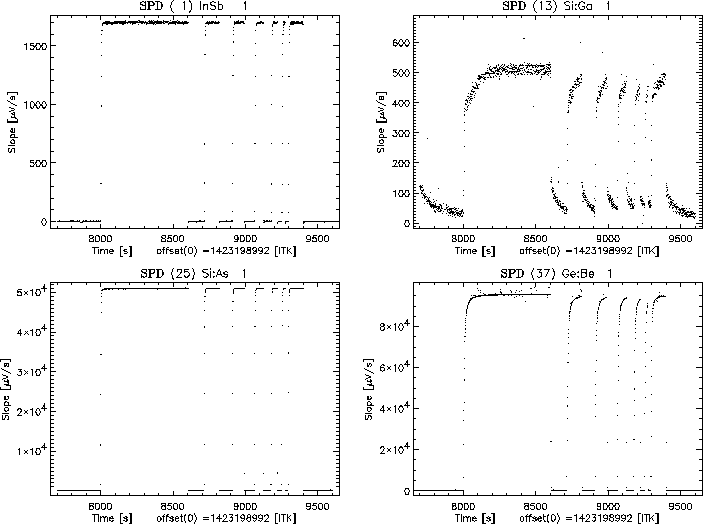 |
The signature of memory effects in the Si:Ga band 2 of SWS is that the up- and down-scans are different in flux level (up to 20% for sources with fluxes greater than about 100 Jy). The down-scan normally succeeds the up-scan in the AOT and appears to be already `accustomed' to the flux level.
For band 2 SWS data, an adapted version of the Fouks-Schubert model was developed by Do Kester (Kester 2001, [98]) and successfully implemented in the legacy version of the SWS pipeline to correct this band for transient effects as well as in the Observers' SWS Interactive Analysis (OSIA) software package (version 3.0). The method brings the errors (sometimes up to 20% originally) down to the few percent level.
A complete description of the procedure followed and how the correction was implemented in the pipeline can be found in the ISO Handbook Volume V on SWS, [108]. Additional details are provided in Kester 2001, [98] and García-Lario et al. 2001, [60].
Several Ge:Ga detectors were also set up for use on board ISO
(see Table 5.3): one detector (P3) and two small
matrix arrays for PHT (C100 3![]() 3 pixels and stressed
C200 2
3 pixels and stressed
C200 2![]() 2 pixels); and several stressed (4) and un-stressed
(5) monolithic detectors for LWS. All of these detectors
were affected by transient effects which can bias the final
photometry typically from 10 to 40%.
2 pixels); and several stressed (4) and un-stressed
(5) monolithic detectors for LWS. All of these detectors
were affected by transient effects which can bias the final
photometry typically from 10 to 40%.
As we have already mentioned, the
present status of our understanding of transients in Ge:Ga detectors is
less favorable than for Si:Ga detectors. Based on the
ratio ![]() , Ge:Ga detectors are unfortunately always
in an unfavourable domain for the application of the
Fouks-Schubert model correction.
, Ge:Ga detectors are unfortunately always
in an unfavourable domain for the application of the
Fouks-Schubert model correction.
At first sight these transients appear easier to model than the
Si:Ga ones because they are at first order exponential
(Church et al. 1993, [22]). Thus, the use of non-linear
models seems to be a priori less necessary in order to take into
account the memory effects. However, the correction is not as precise as the
one obtained for Si:Ga detectors using non-linear models. The expected
accuracy of such simplified analytical models, even if the detector is
perfect, is only about 10-20 ![]() . The main problem is that
some very important characteristics of such detectors are often not well
under control (e.g. contact quality).
and, thus, each Ge:Ga detector seems to require a peculiar model
(Coulais et al. 2000, [36]).
. The main problem is that
some very important characteristics of such detectors are often not well
under control (e.g. contact quality).
and, thus, each Ge:Ga detector seems to require a peculiar model
(Coulais et al. 2000, [36]).
In general, doped germanium detectors show faster stabilisation times than doped silicon ones (typical time scales are 100 s for P3 and C100, 40 s for C200, and 50 to 100 s for LWS detectors). Some of them present an initial hook response (quick overshoot) for high upward steps of flux and undershooting after a downward step. The long term response exhibits a time constant which decreases for high fluxes, whereas it strongly increases for low fluxes. This transient component can be well modelled by an exponential function in most cases (Acosta-Pulido et al. 2000, [8]).
Figures 5.14 and 5.15
show the typical transient behaviour observed in P3
detectors at intermediate and low
flux levels, respectively. We can see the initial hook response clearly in
the intermediate flux example and the longer stabilisation time for low
fluxes. In both cases the long term transient behaviour
has been modelled with a single exponential function which can be written as:

|

|
The first analysis shows that ![]() is inversely proportional to the final
signal,
is inversely proportional to the final
signal, ![]() , in log-log scale (see Acosta-Pulido et al. 2000,
[8]).
Therefore,
, in log-log scale (see Acosta-Pulido et al. 2000,
[8]).
Therefore, ![]() can be written as an inverse power
law function of
can be written as an inverse power
law function of ![]() . The parameter
. The parameter ![]() describes the behaviour of the transient effects with the illumination and
describes the behaviour of the transient effects with the illumination and
![]() is a normalisation constant.
is a normalisation constant. ![]() and
and ![]() are parameters which have
to be determined for each detector/pixel. In the case of the Fouks-Schubert
function
are parameters which have
to be determined for each detector/pixel. In the case of the Fouks-Schubert
function ![]() is equal to unity. If the proposed function is a good
description of the transient behaviour of the considered detectors,
those parameters can be fixed. The stabilised signal is obtained by fitting
the above function to the measured signals and leaving
is equal to unity. If the proposed function is a good
description of the transient behaviour of the considered detectors,
those parameters can be fixed. The stabilised signal is obtained by fitting
the above function to the measured signals and leaving ![]() and
and
![]() as free fit parameters.
as free fit parameters.
The parameters ![]() and
and ![]() for the detectors P3, C100 and C200 were
determined in-orbit using a large set of long measurements. The
measurements were selected if a clear transient behaviour was present,
and they were long enough that at the end the photocurrent is close to
stabilisation. Nevertheless, this data set may suffer some selection bias:
transients with very long time constants (
for the detectors P3, C100 and C200 were
determined in-orbit using a large set of long measurements. The
measurements were selected if a clear transient behaviour was present,
and they were long enough that at the end the photocurrent is close to
stabilisation. Nevertheless, this data set may suffer some selection bias:
transients with very long time constants (![]() 1000 s) could not
be detected because of the limited observing time; and the flux history may
influence the transient as well as the switch-on of the detector every time
an observation starts. In the process of determining
1000 s) could not
be detected because of the limited observing time; and the flux history may
influence the transient as well as the switch-on of the detector every time
an observation starts. In the process of determining ![]() and
and ![]() each measurement was fitted by leaving all parameters free in the
above expression and rejecting those fits where the residual rms per
degree of freedom was larger than 3.
each measurement was fitted by leaving all parameters free in the
above expression and rejecting those fits where the residual rms per
degree of freedom was larger than 3.
The results obtained from a least square fit are presented in Table
5.4, together with the correlation coefficient
![]() . For P3 and C200 the correlation is very good while it is worse for C100.
. For P3 and C200 the correlation is very good while it is worse for C100.
We perfomed tests using an independent set of measurements other than those
used for determining the time constants. The resulting ![]() distributions are very narrow and peak around 1. The worst case is again
the detector C100, for
which the
distributions are very narrow and peak around 1. The worst case is again
the detector C100, for
which the ![]() distribution for all pixels (except pixel 8) is wide
and values around 2-3 are frequent. The low frequency noise which affects
detectors C100 and P3 when measuring faint targets is likely limiting the
goodness of the fit.
distribution for all pixels (except pixel 8) is wide
and values around 2-3 are frequent. The low frequency noise which affects
detectors C100 and P3 when measuring faint targets is likely limiting the
goodness of the fit.
According to the values derived and shown in Table
5.4 it is also possible to estimate
the fraction of the final signal which is affected by the slow
transient component, i.e. the signal difference between the value reached at
the initial jump and the final value. The magnitude of this component
combined with the time constant determines the accuracy of any measurement
after a certain time. For example, a long time constant is not so relevant,
if the fraction of the slow component is small compared to the total signal.
The magnitude of the slow component can be estimated from the initial jump
after a flux change and the knowledge of the final stable current.
This has to be derived from chopped measurements where
the flux changes are like a step-function. Raster observations cannot be
used, because the flux varies gradually as the telescope slews to a different
sky position. Results for detectors P3, C100 and C200 are presented in
Table 5.4, where ![]() represents the fraction
of the total signal
difference which is achieved immediately after the flux change. It has
been found theoretically that the magnitude of the slow component increases
with the photoconductive gain,
represents the fraction
of the total signal
difference which is achieved immediately after the flux change. It has
been found theoretically that the magnitude of the slow component increases
with the photoconductive gain, ![]() (Haegel et al. 1996,
[70]).
(Haegel et al. 1996,
[70]). ![]() depends on the
material, the electric field and the dimensions of the detector. Detectors P3
and C100 are manufactured of the same material but they have different
bias voltages and dimensions, yielding
depends on the
material, the electric field and the dimensions of the detector. Detectors P3
and C100 are manufactured of the same material but they have different
bias voltages and dimensions, yielding ![]()
![]()
![]() ; which is
consistent with a larger fraction of the slow component for C100.
; which is
consistent with a larger fraction of the slow component for C100.
We present in Figure 5.16 an example of the application of this single exponential fit model to a measurement taken with detector C100: using the full measurement time of 512 s an error of 6% between the direct measurement of the signal and the model prediction is found. A comparison of the estimates of the final signal using only the first 32 s gives the following results: the value obtained from the `drift recognition' method which is applied in the pipeline is too low by 30%, whereas the value obtained from the empirical model above described is lower by only 12%. This example demonstrates how the use of this method can significantly improve the photometric accuracy of relatively short measurements.
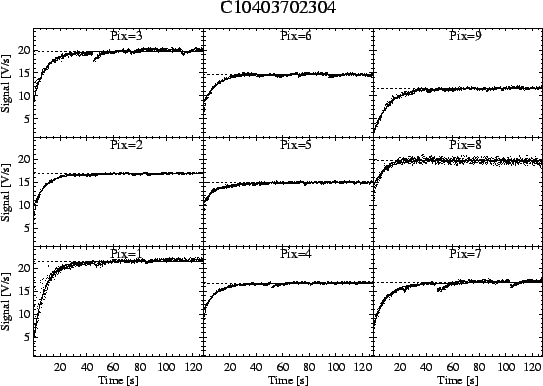
|
Another example, this time applied to detector C200, is shown in Figure 5.17. Again, a single exponential fit has been applied to predict the final signal level with a quite satisfactory result.

|
However, a detailed analysis of the transient curves, especially for detector C100, reveals the presence of more than one time constant. Solutions consisting on a combination of two (and even three) exponential functions have been found to describe better the drifting curve improving the accuracy of the photometry (Church et al. 1996, [23]; Fujiwara et al. 1995, [56]). Currently, several fitting methods are available in the PIA software used for interactive analysis (Gabriel & Acosta-Pulido 1999, [57]). The main difficulty is to determine the relative importance of the different components.
In the pipeline, a simple `drift recognition' method similar to the one applied in Si:Ga detectors is implemented for PHT-P3 and PHT-C staring observations. If the stability test fails for a given measurement, a empirical solution based on the fitting of an exponential function is tried (Schulz et al. 2002, [148]). Thus, as for the PHT-P1 detectors, the transient correction applied only works satisfactorily for measurements which are long compared to the detector stabilisation time at a given illumination.
In the case of chopped measurements, where non-stabilised signal
causes significant losses to the true difference signal, OLP makes use of a
`pattern recognition' method similar to the one used also for PHT-P1
detectors. For P3 detectors the accuracy is poor when the fluxes
are below between 0.2 and 1 Jy (the exact number depends on aperture size
and chopper throw), due
to cirrus confusion and the restricted number of sky references longward of
80 ![]() m. For C100 and C200 the accuracy is also strongly limited when the
fluxes detected are below 0.2 Jy and 1 Jy, respectively. In this case
the chopper offset correction, being the zero point of the signal
correction, is less accurate and the relatively bright sky background and
the small number of reference positions make an estimation of the
cirrus confusion noise necessary.
m. For C100 and C200 the accuracy is also strongly limited when the
fluxes detected are below 0.2 Jy and 1 Jy, respectively. In this case
the chopper offset correction, being the zero point of the signal
correction, is less accurate and the relatively bright sky background and
the small number of reference positions make an estimation of the
cirrus confusion noise necessary.
Finally, no transient correction was implemented in the pipeline for PHT32 chopped raster maps because of the high interactivity needed in the processing to correct these maps for transient effects. A processing tool including full transient modelling developed by Richard Tuffs (from MPI-Heidelberg) is available in PIA and details on its application to real data can be found in the proceedings of the ISOPHOT Workshop on P32 Oversampled Mapping, [149].
LWS Ge:Ga detectors present also memory effects, due to their
slow response times (typically tens of seconds, as already mentioned) to
changes of illumination (Church et al. 1992, [21]).
As for the other Ge:Ga detectors on board ISO the typical
transient behaviour of both LWS stressed and unstressed detectors
consists of a long term component due to the
steady accumulation of particle hits during each revolution and a short
term component caused by the changes in flux.
In general, after a flux change, the immediate reaction is quick, and in some cases the detector overshoots, producing the characteristic hook response, but the detector output can take a considerable time to settle the final level. Specific laboratory tests were made before launch (Church et al. 1996, [23]) showing that the detectors actually react on a variety of time scales depending on the initial and final flux levels.
Church et al. 1996, [23]
found that the response of LWS Ge:Ga detectors to a step
change in flux could be modelled empirically by a function containing
three exponential time constants, with typical values of
![]() 1, 5 and 30 seconds (for unstressed Ge:Ga detectors) and 0, 10 and 100
seconds (for stressed Ge:Ga detectors). However, the general behaviour and
appearance of the
hook response depends on bias and operating temperature, as well as on the
flux levels. The main difference between the stressed and unstressed
Ge:Ga detectors is in the speed of the hook response (faster in the
stressed Ge:Ga detectors). The time constants
generally decrease with increasing flux step. In all cases the
transient response after a decreasing flux step is faster than the
response after an increasing flux step. Kaneda et al. 2001,
[92] uses
a step and two-component exponential model to fit the step response of
these detectors and shows that the transient response time decreases with an
increase in both the initial and final incident flux levels.
1, 5 and 30 seconds (for unstressed Ge:Ga detectors) and 0, 10 and 100
seconds (for stressed Ge:Ga detectors). However, the general behaviour and
appearance of the
hook response depends on bias and operating temperature, as well as on the
flux levels. The main difference between the stressed and unstressed
Ge:Ga detectors is in the speed of the hook response (faster in the
stressed Ge:Ga detectors). The time constants
generally decrease with increasing flux step. In all cases the
transient response after a decreasing flux step is faster than the
response after an increasing flux step. Kaneda et al. 2001,
[92] uses
a step and two-component exponential model to fit the step response of
these detectors and shows that the transient response time decreases with an
increase in both the initial and final incident flux levels.
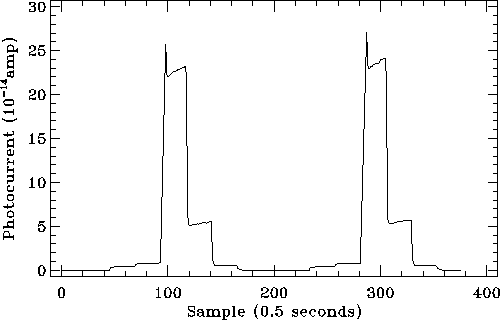
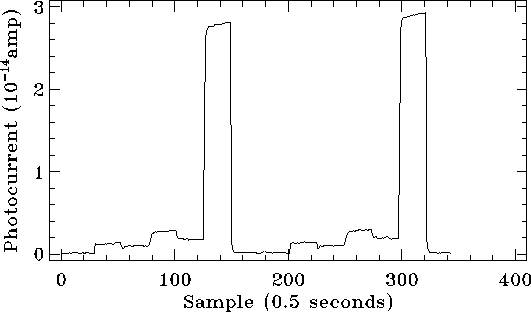
The in-orbit transient response of the detectors is most clearly seen in the illuminator flashes that provide the basic sensitivity drift calibration. These are steps in flux levels that mirror the laboratory tests, but these sequences are much shorter and not all the effects appear as described above. Sample illuminator flashes are shown in Figures 5.18 and 5.19 for detectors SW4 (unstressed Ge:Ga) and LW2 (stressed Ge:Ga) respectively, which are those affected by the largest transient effects. For these detectors the slow long term response is the main problem as the flux is still increasing at the end of the flash. SW3 (unstressed Ge:Ga) and LW4 (stressed Ge:Ga) also show the same effect to a lesser extent. The remaining detectors are rather better behaved, e.g. the stressed LW5 (see Figure 5.20), although LW1 (unstressed) and LW3 (stressed) invariably show also a hook response.
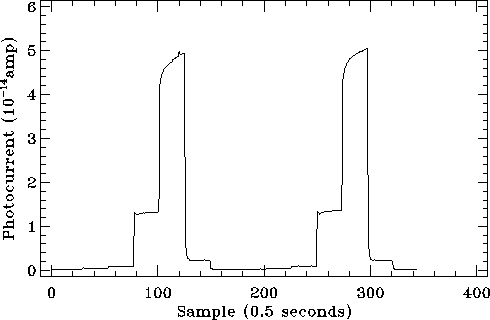
|
|
The effect of the detector transient response on the illuminator flashes is to introduce a non-linearity into the drift correction. The problem is not that the correct illuminator flash level is not reached, but that the detector will respond differently depending on the flux levels involved, so the calibration will be inconsistent. How inconsistent will depend on the change in flux levels and the severity of the detector transient response.
|
One of the major effects of this transient behaviour is in the determination and application of the so-called `Relative Spectral Response Function' (RSRF). LWS was operated in a mode where the grating was scanned forward and backward through the spectral range. For most detectors the scans pass through steep sided RSRFs and the resultant profiles are clearly split with the photocurrent dependent on scan direction. The transient response of the detectors can be seen in the difference in flux level between forward and backward scans. In general this leads to a distortion of the whole grating profile and of individual line profiles.
The calibration strategy used in the pipeline for the derivation of the LWS RSRF for a given detector was to average all data before dividing by the Uranus model. However when this averaged RSRF is applied in the pipeline it leads to a scan dependent behaviour in the resultant spectra.
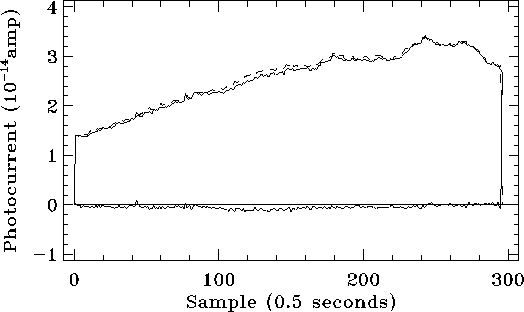
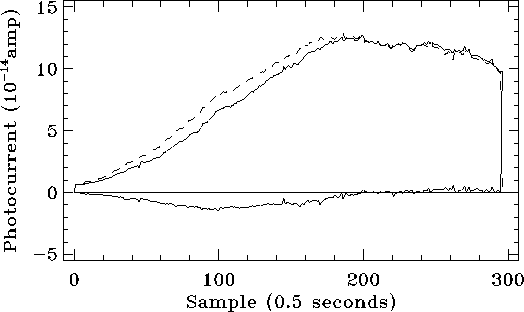
Figures 5.21 and 5.22 show the spectrum of Uranus as observed by the SW4 (unstressed Ge:Ga) and LW2 (stressed Ge:Ga) detectors, respectively. We can see that LW2 does show significant differences between the forward and backward scans, while SW4 does not, possibly because of the lower fluxes and the smaller flux changes involved.
|
|
The transient behaviour of the LWS detectors can also affect the line flux accuracy. The effect, however, is minor (a few percent) in grating spectra and it has only been detected in the stressed Ge:Ga detectors, where it is found to depend on both the line flux and the illumination history.
In the case of Fabry-Pérot observations made with LWS,
the line profiles observed using AOT LWS04 are
generally asymmetric, with the long wavelength wing at a higher flux
level than the short wavelength one. The effect
on line flux depends on the line-to-continuum ratio. For example, for a line
with no continuum, the line flux can change by as much as 30%.
The effect on the velocity shift is relatively small (about ![]() 3 km
s
3 km
s![]() ). It is also possible that some of the asymmetry observed
may be due to loss of parallelism as the Fabry-Pérot line is scanned.
). It is also possible that some of the asymmetry observed
may be due to loss of parallelism as the Fabry-Pérot line is scanned.
Various methods for removal of transient effects in LWS detectors have been investigated.
Linear models based on fitting two or three exponentials do not work on a wide dynamical range of these detectors. While it is possible to construct an empirical fit to the transient response of the detectors with a two- or three-component exponential function, the reality is probably more complicated.
There have also been several attempts to provide a physically realistic model of doped germanium detectors able to account for their non-linear behaviour. However, these models are extremely complex and, thus, it is worth to try using analytical simplifications like the Fouks-Schubert model applied to the Si:Ga detectors.
The problem is that the Fouks-Schubert model, as we have already mentioned, is in principle not applicable to Ge-based detectors. In spite of this, a modified version of the Fouks-Schubert model has been developed and applied to several bands of LWS with relative success (Caux 2001, [15]). The routine used to find the Fouks-Schubert parameters is stable, but it still remains to check posible dependences on the spectral shape of the source.
For the time being, and before a solution is given to some still existing problems affecting the determination of the LWS RSRF using the adapted Fouks-Schubert model, a simple method to correct the fluxes has been developed which assumes that the slow upward changes in flux have a single time constant and that the downward changes are instantaneous, reflecting the differences seen in the laboratory experiments and illuminator sequences (Lloyd 2001c, [118]). The time constant is chosen so as to minimise the differences between the forward and backward scans. An example of the results obtained this way is shown in Figure 5.23.

|
Another possible approach to correct for these memory effects is to use two RSRF functions, each derived only from scans in one direction. Attempts using this calibration strategy have so far led also to promising results.
Unfortunately, no correction is done for transient effects as such in the LWS pipeline. However, there is a plan to include a dedicated routine to perform this correction in the future in the LWS Interactive Analysis (LIA) software package based on new transient effect corrected RSRFs obtained using the adapted Fouks-Schubert model above mentioned. These new RSRFs differ by just a few percent with respect to the old ones. Some preliminary results on the application of this correction to grating and Fabry-Pérot LWS observations can be found in Caux 2001, [15], where the implications on line flux calibration, wavelength calibration and spectral resolution are discussed.
Meanwhile, efforts on improving the pipeline products have concentrated in finding a correction for the effects observed in the illuminator flashes. Although the illuminator flashes, especially the brightest ones, are not flat, they are very consistent in shape, within the constraints of the transient response. When calculating the drift correction, which is a ratio of the observed illuminator flash to the `standard' one, it is therefore important to use a method that recognises this consistency. The most appropriate method is the one that calculates the ratio on a point-by-point basis. This weighted-average method (explained in detail in Sidher et al. 2001, [150]) is applied in OLP Version 10 to process the illuminator flashes and represents a considerable improvement with respect to previous OLP versions but, unfortunately, it is only valid for the longer duration of the new style of flashes performed after revolution 442. The shorter duration of the old style flashes in observations before ISO revolution 442 often leaves just 3 to 4 points for an individual illuminator, following removal of data points affected by glitches, thus making it almost impossible to apply this method. It is important to note that in OLP Version 10, data from the old style flashes is still processed using the old method and, thus, they are expected to be more affected by transients.
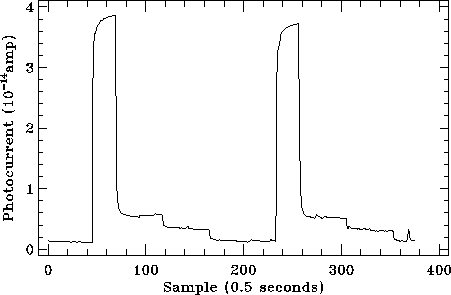
The SW CAM CID In:Sb 32![]() 32 matrix array is also affected by
a strong transient effect but without instantaneous jump (
32 matrix array is also affected by
a strong transient effect but without instantaneous jump (![]() =0), as it
can be seen in Figure 5.24. The
time lag when responding to a flux variation is attributed to the surface
traps in the detector, which need to be filled first with photon-generated
charges before the well begins to actually accumulate signal
(Tiphène et al. 1999, [157]).
=0), as it
can be seen in Figure 5.24. The
time lag when responding to a flux variation is attributed to the surface
traps in the detector, which need to be filled first with photon-generated
charges before the well begins to actually accumulate signal
(Tiphène et al. 1999, [157]).
|
Although a detailed physical model of this transient behaviour is lacking an empirical model has been developed which reproduces quite well the observed response using only a small set of parameters. The model provides the asymptotic value of the stabilised signal. Unfortunately, because of the limited number of test cases available it is difficult to judge whether the method is generally applicable to the full range of SW CAM data.
PHT-P2 (Si:B) is also affected by transients. An example of
P2 detector transients induced by chopper modulation
are shown in Figure 5.25.
As we can see they also may exhibit a hook response or overshoot
after large positive flux steps, like other doped silicon detectors,
followed by a slow decay.

|
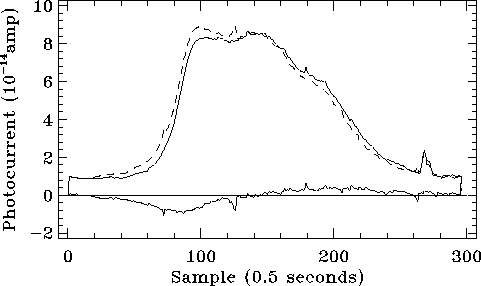
Figure 5.26 shows the response to an
illuminator sequence of the Ge:Be detector SW1 of LWS.
This detector is the worst
affected by transients in LWS, and exhibits a longer time constant
(several minutes) compared to the above described LWS Ge:Ga detectors, which
decreases with increasing flux step.
|
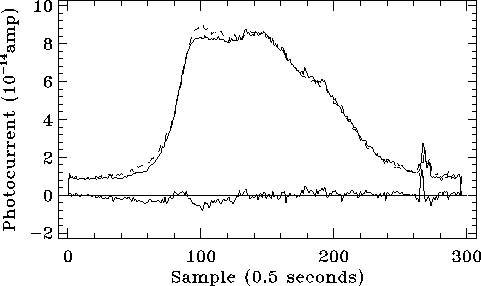
Like other LWS detectors, SW1 also shows significant differences
between the forward and backward scans (see Figure
5.27), affecting the spectrum profile
and the line flux accuracy, although very few bright lines are observed
in the wavelength range covered by this detector (43-51 ![]() m).
m).
|
The response of the detector to a step change in flux can also be modelled empirically by a function containing three exponential time constants, with typical values of 5, 20 and 200 seconds (Church et al. 1996, [23]) but, again, the initial hook response cannot be reproduced.
Moreover, the adapted Fouks-Schubert model used for the Ge:Ga detectors with relative success simply does not work in this case.
Significant improvements, however, are achieved with the help of the same simple model that was applied to the Ge:Ga detectors (Lloyd 2001, [118]) which assumes that the slow upward changes in flux have a single time constant and that the downward changes are instantaneous, with the time constant chosen as to minimise the difference between backward and forward scans. Figure 5.28 shows the result of applying this simple model to the SW1 spectrum of Uranus used to derive the detector RSRF.
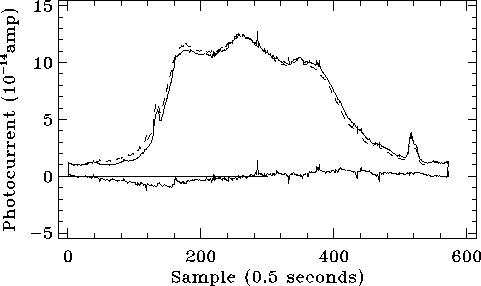
|
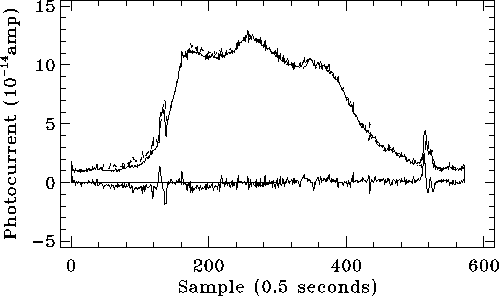
The observations of NGC6302 provide a slightly different test. The means of the forward and backward scans in SW1 are shown in Figure 5.29 where large differences are also observed, similar to those observed in Uranus. The corrected data are shown in Figure 5.30.
|
|
It is clear that this simple model does provide some correction to the data, particularly to the slower changes in flux, but it can still be improved.
Band 4 (Ge:Be) and the two Fabry-Pérot bands (Si:Sb and Ge:Be) of SWS
are also affected by memory effects (Wensink et al. 1992,
[164]).
Concerning band 4, we know that the Fouks-Schubert model does not work in Ge:Be detectors and up to now, no efficient model has been found to describe these memory effects. As a consequence of this, no correction for memory effects in this band is applied in the pipeline. Efforts are, however, still on-going to try to find an alternative method.
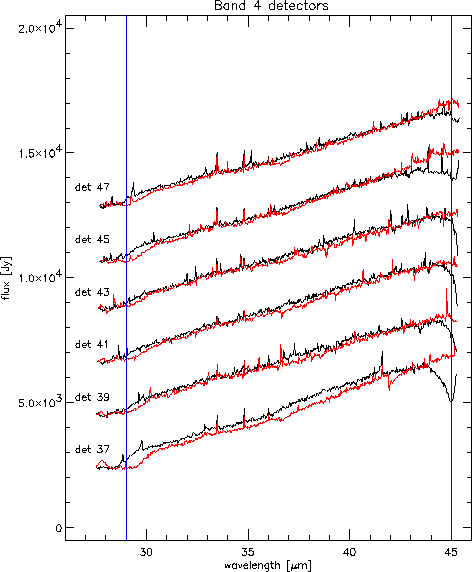
An example of the various effects seen in band 4 is shown in Figure 5.31, an SWS01 speed 4 observation of K3-50. At the start of the up-down scan (at the longer wavelength side) we see a transient. Some detectors, like 37, display a hook effect, some rise faster than others, seeming to get earlier to their relaxed state than the others. At the shorter wavelength there also seems to be some hysteresis effect, where the second part (the down scan in red) seems to stall before getting into the rising mood.
On the other hand, the consequences of transients in the Fabry-Pérot bands (FP in Table 5.3) appear at the present time limited. The main reason for this is that most flux passing through the FP's is weak, in the flux domain where transients are not yet so important. Moreover, FPs could only be operated in one direction, which prevented the up-down strategy to correct for transients. So unless we assume that the FP lines are always symmetrical, or better, that the FP spectrum itself has some a priori known characteristics, we cannot disentangle the transients from the spectrum. Thus, a transient correction was never applied.
|
Other detectors on board ISO are completely free of transient effects. This is the case of band 1 (In:Sb) and band 3 (Si:As BIBIB) of SWS (see Figure 5.13).